2. 正弦波の複素数表示 - 趣味人のブログ

本章では，先ず 2.1 において複素数の極形式と複素指数関数を復習する．次に 2.2 において正弦波のベクトル表示と複素数表示が等価である事を示す．そして 2.3 以降において，極形式による正弦波の複素数表示の利点として，正弦波に対する種々の計算が容易になる事を述べる．

尚，本資料では虚数単位を j とする．また，複素数 α = A + jB の実部，虚部，絶対値，偏角，共役複素数を示す関数を以下の通り定義する．

$\begin{matrix} (2-1) & \begin{matrix} \begin{matrix} R e (α) = A \\ I m (α) = B \\ |α| = \sqrt{A^{2} + B^{2}} \\ A r g (α) = {t a n}^{- 1} (\frac{B}{A}) \\ \overline{α} = A - j B \end{matrix} \end{matrix} \end{matrix}$

2.1. 複素数の極形式と複素指数関数
2.2. 極形式による正弦波の複素数表示
2.3. 正弦波の位相の進み遅れ
2.4. 正弦波の時間微分と積分
- 振幅によって表示された正弦波の時間微分と積分
- 複素数表示による正弦波の時間微分と積分
2.5. 角周波数が等しい正弦波の合成
2.6. 正弦波の複素数表示の適用範囲
参考: 複素指数関数による正弦波の記述

2.1. 複素数の極形式と複素指数関数

高校数学で学習した通り，絶対値が r 偏角が θ となる複素数 α は以下の極形式 (極表示，極形式表示とも呼ばれる) で表示する事が出来る．

$\begin{matrix} (2-2) & α = r (c o s θ + j s i n θ) \end{matrix}$

オイラーの公式 e ^jθ = cos θ + j sin θ により，上記の式は以下の複素指数関数で表示する事ができる．これも複素数の極形式と呼ばれる．

$\begin{matrix} (2-3) & α = r (c o s θ + j s i n θ) = r e^{j θ} \end{matrix}$

これらの関係を以下の複素数平面に示す．

f:id:suzumushi0:20170604143542p:plain — **図2-1: 複素数の極形式表示．**

複素指数関数による，複素数の極形式表示の利点は，複素数の積を容易に計算できる点にある．複素指数関数では，実数の指数関数と同様の指数法則 e ^a^+b= e ^ae ^bが成立する．このため，絶対値が r₁ 偏角が θ₁，及び絶対値が r₂ 偏角が θ₂ となる複素数の積は以下の様に容易に求める事ができる．

$\begin{matrix} (2-4) & r_{1} e^{j θ_{1}} r_{2} e^{j θ_{2}} = r_{1} r_{2} e^{j (θ_{1} + θ_{2})} \end{matrix}$

即ち，複素指数関数で表示された複素数の積の絶対値および偏角は，各々複素指数関数の絶対値の積および偏角の和となる．尚，実数の指数関数と異なり，複素指数関数は周期 2π の周期関数となる．

Note: ベクトルの和や差と複素数の和や差には対応関係があるが，ベクトルの内積，外積と複素数の積は異なる概念である．

2.2. 極形式による正弦波の複素数表示

次に，正弦波のベクトル表示は複素数表示と等価となる事を示す．1.1に述べた通り，振幅が A，角周波数が ω，初期位相が φ，位相が (ωt + φ) となる正弦波は，以下の成分の回転ベクトルで表示する事ができる．

$\begin{matrix} (2-5) & P (t) = (A c o s (ω t + φ), A s i n (ω t + φ)) \end{matrix}$

1 章に述べた正弦波のベクトル表示の説明では，ベクトルに対する操作は分解，合成のみが用いられている．ここで，ベクトルの和や差は，ベクトルの各成分の和や差となり，複素数の和や差は，複素数の実部と虚部同志の和や差となる．従って，図1-2 に示した直交座標における正弦波の回転ベクトル表示を，下図の様に複素数平面に表示しても，1章と同様の説明が成立する事は明らかである．

f:id:suzumushi0:20170604143543p:plain — **図2-2: 正弦波の複素数表示．**

振幅が A，角周波数が ω，初期位相が φ，位相が (ωt + φ) となる正弦波の複素数表示 z (t) を以下に示す．

$\begin{matrix} (2-6) & z (t) = A c o s (ω t + φ) + j A s i n (ω t + φ) \end{matrix}$

正弦波の回転ベクトル表示と同様に，z (t) は，振幅 A を絶対値，位相 (ωt + φ) を偏角とする極形式の複素数を，複素数平面に表示したものである．ここで，虚数単位 j は 2 次元の座標を一つの複素数として表示するために便宜的に用いられているだけであり，理論上，想像上の数である虚数によって計測される物理的現象が存在する事を示している訳では無い．上記は正弦波の回転ベクトル表示と等価であり，振幅が A，位相が (ωt + φ) の正弦波という物理的現象を表示したものである．

オイラーの公式 e ^jθ = cos θ + j sin θ より，振幅がA，角周波数が ω，初期位相が φ，位相が (ωt + φ) となる正弦波の複素数表示は，以下の複素指数関数による極形式表示で表す事ができる．

$\begin{matrix} (2-7) & z (t) = A c o s (ω t + φ) + j A s i n (ω t + φ) = A e^{j (ω t + φ)} \end{matrix}$

即ち，極形式表示の絶対値が振幅を，偏角が位相を示す．指数法則により，上記の複素指数関数による極形式は，下記の通り分解できる．

$\begin{matrix} (2-8) & z (t) = A e^{j (ω t + φ)} = A e^{j φ} e^{j ω t} \end{matrix}$

また，正弦波の変位 y (t) は以下で与えられる．

$\begin{matrix} (2-9) & \begin{matrix} \begin{array}{r} y (t) \end{array} \begin{array}{l} = I m \{z (t)\} \\ = I m \{A e^{j (ω t + φ)}\} \\ = I m \{A c o s (ω t + φ) + j A s i n (ω t + φ)\} \\ = A s i n (ω t + φ) \end{array} \end{matrix} \end{matrix}$

ここで，時間 t = 0 の際の極形式による正弦波の複素数表示を以下に示す．

$\begin{matrix} (2-10) & z (0) = A e^{j φ} = A \cos φ + j A \sin φ \end{matrix}$

正弦波の静止ベクトル表示と同様に，z (0) は，振幅 A を絶対値，初期位相 φ を偏角とする極形式の複素数を，複素数平面に表示したものである．

Note: 上記の振幅を交流の実効値に置き換えると，電気工学における交流のフェーザ表示となる．

以上の極形式による正弦波の複素数表示を図2‑3に示す．2.1 に述べた通り，複素数の積の偏角は，偏角の和となるから，z (t) は，下の図に示す様に，z (0) = A e ^jφが ωt だけ回転したものと見做す事が出来る．

f:id:suzumushi0:20170604143544p:plain — **図2-3: 極形式による正弦波の複素数表示．**

Note: 極形式による正弦波の複素数表示において，振幅，初期位相を表示する A e ^jφは単なる係数であるから，議論を簡略化するため，振幅が 1，角周波数が ω，初期位相が 0 となる正弦波 e ^jωt のみを議論する場合がある．e ^jωt は複素正弦波と呼ばれる．

2.3. 正弦波の位相の進み遅れ

極形式による正弦波の複素数表示によって，以下に示す通り，正弦波の位相の進みや遅れを簡易に表示する事が出来る．何れも基準となる正弦波は e ^jωtとする．

θ の位相進み

2.1 に述べた通り，複素数の積の偏角は，偏角の和となるから，θ の位相進みは e ^jωtに対して e ^jθを乗ずる事で得られる．

$\begin{matrix} (2-11) & e^{j (ω t + θ)} = e^{j θ} e^{j ω t} \end{matrix}$

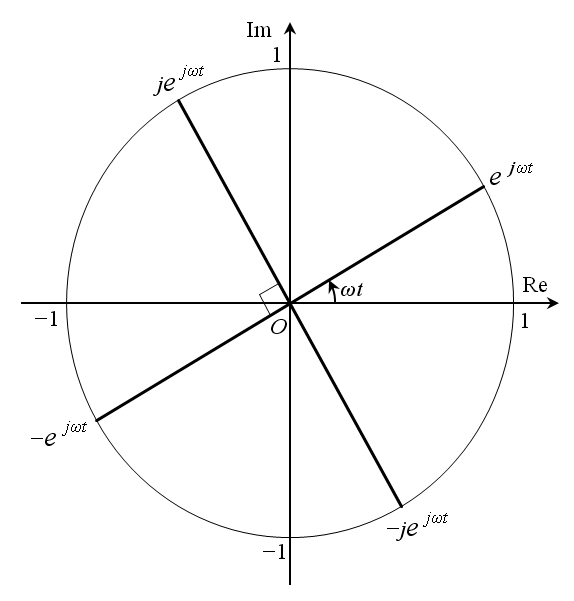
特に，以下に示す通り π / 2 の位相進みは j，逆相は − 1，π / 2 の位相遅れは − j を乗ずる事で得られる．

π / 2の位相進み

$\begin{matrix} (2-12) & e^{j (ω t + \frac{π}{2})} = e^{j ω t} e^{j \frac{π}{2}} = e^{j ω t} (\cos \frac{π}{2} + j \sin \frac{π}{2}) = j e^{j ω t} \end{matrix}$

逆相 (π の位相進み)

$\begin{matrix} (2-13) & e^{j (ω t + π)} = e^{j ω t} e^{j π} = e^{j ω t} (\cos π + j \sin π) = - e^{j ω t} \end{matrix}$

π / 2の位相遅れ

$\begin{matrix} (2-14) & e^{j (ω t - \frac{π}{2})} = e^{j ω t} e^{j (- \frac{π}{2})} = e^{j ω t} \{\cos (- \frac{π}{2}) + j \sin (- \frac{π}{2})\} = - j e^{j ω t} \end{matrix}$

以上の関係を下の図に示す．

f:id:suzumushi0:20170604143545p:plain — **図2-4: 極形式による正弦波の位相の進み，遅れ．**

2.4. 正弦波の時間微分と積分

極形式による正弦波の複素数表示によって，正弦波の時間微分や積分を簡易に計算する事が出来る．

振幅によって表示された正弦波の時間微分と積分

先ず，振幅によって表示された下記の正弦波の時間微分と積分を考える．

$\begin{matrix} (2-15) & y (t) = A s i n (ω t + φ) \end{matrix}$

上記の正弦波の時間微分を以下に示す．以下の式において θ = ωt + φ である．

$\begin{matrix} (2-16) & \begin{matrix} \begin{array}{r} \frac{d}{d t} A s i n (ω t + φ) \end{array} \begin{array}{l} = A \frac{d}{d t} θ \frac{d}{d θ} s i n θ \\ = ω A c o s θ \\ = ω A s i n (ω t + φ + \frac{π}{2}) \end{array} \end{matrix} \end{matrix}$

上から明らかな通り，正弦波を時間微分すると正弦波となり，角周波数は変化せず，振幅は ω 倍，かつ位相は π / 2 進む．次に上記の正弦波の時間積分を以下に示す．以下の式において θ = ωt + φ である．

$\begin{matrix} (2-17) & \begin{matrix} \begin{array}{r} \int A s i n (ω t + φ) d t \end{array} \begin{array}{l} = A \int s i n θ (\frac{d t}{d θ}) d θ \\ = \frac{A}{ω} \int s i n θ d θ \\ = - \frac{A}{ω} c o s θ + C \\ = \frac{A}{ω} s i n (ω t + φ - \frac{π}{2}) + C \end{array} \end{matrix} \end{matrix}$

ここで C は積分定数である．上記から明らかな通り，積分定数が無視できる場合，正弦波を時間積分すると正弦波となり，角周波数は変化せず，振幅は1 / ω 倍，かつ位相は π / 2 遅れる．

複素数表示による正弦波の時間微分と積分

次に，上記と等価な複素数表示による下記の正弦波の時間微分と積分を考える．

$\begin{matrix} (2-18) & z (t) = A e^{j (ω t + φ)} \end{matrix}$

上記の正弦波の時間微分を以下に示す．

$\begin{matrix} (2-19) & \begin{matrix} \begin{array}{r} \frac{d}{d t} A e^{j (ω t + φ)} \end{array} \begin{array}{l} = A e^{j φ} \frac{d}{d t} e^{j ω t} \\ = j ω {A e^{j φ} e}^{j ω t} \\ = j ω A e^{j (ω t + φ)} \end{array} \end{matrix} \end{matrix}$

前に述べた通り，j は π / 2 の位相進みを表すから，正弦波を時間微分すると正弦波となり，角周波数は変化せず，振幅は ω 倍，かつ位相は π / 2進み，三角関数による時間微分と一致する．即ち，正弦波の複素数表示では，時間微分は jω を乗ずる事で得られる．次に上記の正弦波の時間積分を以下に示す．

$\begin{matrix} (2-20) & \begin{matrix} \begin{array}{r} \int A e^{j (ω t + φ)} d t \end{array} \begin{array}{l} = A e^{j φ} \int e^{j ω t} d t \\ = {\frac{A}{j ω} e^{j φ} e}^{j ω t} + C \\ = - j \frac{A}{ω} e^{j (ω t + φ)} + C \end{array} \end{matrix} \end{matrix}$

ここで C は積分定数である．前に述べた通り − j は π / 2 の位相遅れを表すから，積分定数が無視できる場合，正弦波を時間積分すると正弦波となり，角周波数は変化せず，振幅は 1 / ω 倍，かつ位相は π / 2 遅れ，三角関数による時間積分と一致する．即ち，正弦波の複素数表示では，時間積分は，積分定数が無視できる場合は，− j / ω を乗ずる事で得られる．

2.5. 角周波数が等しい正弦波の合成

極形式による正弦波の複素数表示による，角周波数が等しい正弦波の合成 (一次結合，線形結合) を示す．以下の通り 1.3 と同じ正弦波の合成を考える．

$\begin{matrix} (2-21) & \begin{matrix} \begin{matrix} z_{1} (t) = A_{1} e^{j (ω t + φ_{1})} \\ {z_{2} (t) = A}_{2} e^{j (ω t + φ_{2})} \end{matrix} \end{matrix} \end{matrix}$

上記の正弦波の合成を以下に示す．

$\begin{matrix} (2-22) & \begin{matrix} \begin{array}{r} z_{1} (t) + z_{2} (t) \end{array} \begin{array}{l} = A_{1} e^{j (ω t + φ_{1})} + A_{2} e^{j (ω t + φ_{2})} \\ = A_{1} e^{j φ_{1}} e^{j ω t} + A_{2} e^{j φ_{2}} e^{j ω t} \\ = (A_{1} e^{j φ_{1}} + A_{2} e^{j φ_{2}}) e^{j ω t} \\ = \{(A_{1} c o s φ_{1} + A_{2} c o s φ_{2}) + j (A_{1} s i n φ_{1} + A_{2} s i n φ_{2})\} e^{j ω t} \end{array} \end{matrix} \end{matrix}$

ここで，e ^jωtは振幅が 1，角周波数が ω，初期位相が 0 となる複素正弦波を表示している．またこれの係数は振幅と初期位相を表示し，式 (1‑16) おける合成された正弦波の静止ベクトル表示と等価となる．よって，合成した正弦波の角周波数は ω となり，1.3と同様に振幅 A，初期位相 φ は以下の式で与えられる．

$\begin{matrix} (2-23) & A = \sqrt{{A_{1}}^{2} + {A_{2}}^{2} + 2 A_{1} A_{2} \cos (φ_{1} - φ_{2})} \end{matrix}$ $\begin{matrix} (2-24) & φ = \tan^{- 1} \frac{A_{1} s i n φ_{1} + A_{2} s i n φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}} \end{matrix}$

2.6. 正弦波の複素数表示の適用範囲

以上，極形式による正弦波の複素数表示によって，位相の進みや遅れ，時間微分や積分，角周波数が等しい正弦波の合成を容易に計算，表示出来る事を示した．しかし，うまい話には必ず裏がある．実はこの表示方法の適用範囲は，計算によって正弦波の角周波数が変化しない場合に限定される．振幅と初期位相は変化しても構わない．本資料に述べた位相の進みや遅れ，時間微分や積分，角周波数が等しい正弦波の合成では正弦波の角周波数はいずれも変化しない．

一方，この表示方法は，計算結果が，正弦波以外の波形となる場合や，角周波数が異なる正弦波となる場合には適用出来ない．この例として正弦波の積がある．正弦波同士の積は正弦波にはならない (角周波数が元の正弦波の角周波数の和と差になる2つの正弦波の重ね合わせとなる) ため下記の様な用法は誤りとなる．

$\begin{matrix} (2-25) & A_{1} e^{j (ω_{1} t + φ_{1})} A_{2} e^{j (ω_{2} t + φ_{2})} = A_{1} A_{2} e^{j (φ_{1} + φ_{2})} e^{j (ω_{1} + ω_{2}) t} \end{matrix}$

Note: 2.3 に述べた位相の進み遅れにおける定数係数の複素数の積と上記を混同しない事．時間関数となる正弦波同士の積に適用できないのである．

この表示方法が適用できる対象は，具体的には，入出力の関係が定数係数線形常微分方程式で記述されるシステムとなる．これの詳細に関しては 4章以降において詳しく述べる．尚，次の 3 章の内容は全てこの条件を満足しているため，この点を気にする必要は無い．

参考: 複素指数関数による正弦波の記述

本章に示した極形式による正弦波の複素数表示と異なる正弦波の記述方法として，複素指数関数による正弦波の記述がある．オイラーの公式 e ^jθ = cos θ + j sin θ により，cos θ 及び sin θ は以下の様に複素指数関数で表示する事ができる．

$\begin{matrix} (2-26) & \begin{matrix} \begin{matrix} c o s θ = \frac{e^{j θ} + e^{- j θ}}{2} \\ s i n θ = \frac{e^{j θ} - e^{- j θ}}{j 2} = - j \frac{e^{j θ} - e^{- j θ}}{2} \end{matrix} \end{matrix} \end{matrix}$

従って，時間 t に観測された変位が y (t)，振幅が A，角周波数が ω，初期位相が φ，位相が (ωt + φ) となる正弦波は，以下の様に複素指数関数で表示する事ができる．

$\begin{matrix} (2-27) & \begin{matrix} \begin{array}{r} y (t) \end{array} \begin{array}{l} = A s i n (ω t + φ) \\ = A c o s φ s i n (ω t) + A s i n φ c o s (ω t) \\ = A \frac{e^{j φ} + e^{- j φ}}{2} \frac{e^{j ω t} - e^{- j ω t}}{j 2} + A \frac{e^{j φ} - e^{- j φ}}{j 2} \frac{e^{j ω t} + e^{- j ω t}}{2} \\ = A \frac{e^{j φ} e^{j ω t} - e^{- j φ} e^{- j ω t}}{j 2} = A \frac{e^{j (ω t + φ)} - e^{- j (ω t + φ)}}{j 2} \end{array} \end{matrix} \end{matrix}$

上記は正弦波の複素数表示 A e^j^{(ωt + φ)} と，これと共役な複素数 A e^−j^{(ωt + φ)} に基づいた正弦波の記述と考える事もできる．この場合，後者の共役複素数は，下図に示す様に，時間 t の経過と共に時計回りに角周波数 ω で回転する理論上，想像上の正弦波となり，負の周波数と呼ばれる．

f:id:suzumushi0:20170604143546p:plain — **図2-5: 負の周波数．**

正弦波の極形式による複素指数表示と，上記に示した複素指数関数による正弦波の記述は，各々複素数平面と直交座標における正弦波の記述方法であるため，これらを混在させない事をお勧めする．正弦波を複素指数表示で記述したにも係わらず，正弦波の変位を複素指数関数による正弦波で記述している例が散見されるが，この場合は変位に負の周波数 A e^−j^{(ωt + φ)}が出現する事の説明が付かなくなる．

本資料で何回も述べている通り，正弦波の極形式による複素指数表示とは，数式の表現上では複素指数関数というあたかも一つの数値であるかの様に表示しているだけで，それの実態は正弦波のベクトル表示と論理的に等価な，実部と虚部からなる只の複素数であり，その虚部は変位を示すのであるから，それを変位とすれば良いのである．