球散乱効果フィルタ - 趣味人のブログ

本ドキュメントは球散乱効果フィルタの詳細を述べる．球散乱効果フィルタは，剛体球への入射波を入力とし，球による散乱波と入射波を出力する．SoundObject では球散乱効果フィルタによって左右方向の距離感を実現している．剛体球による散乱の厳密解は煩雑であるため，2 重音源による近似解を提案する．次に，提案した近似に基づいた球散乱効果によるフィルタの周波数特性や指向特性を求める．最後に，球散乱効果を実現するディジタルフィルタの設計と評価を述べ，両耳間時間差，レベル差による効果と比較して，より明確な距離感が得られる事を明らかにする．

1. 剛体球による散乱

Fig. 1 に示す通り，原点を中心とする半径 a の剛体球に対して，平面波が x 軸に向かって負の方向に伝搬する．また，G (jω) を平面波の音圧に対して球の表面で観測される音圧の比を示す周波数伝達関数とする．座標 (r, θ₀) で観測される入射波と球からの散乱波による音場から G (jω) を求める．この場合，散乱波の仮想的な音源の位置は原点となる．本ドキュメントでは j を虚数単位，t を時間，c を音速，ω を角周波数，k を波数 (k = ω/c)，ρ を媒質密度とする．

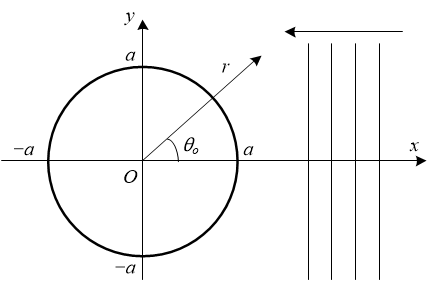
f:id:suzumushi0:20210807154509p:plain — **Fig. 1: Scattering by a rigid sphere.**

Note: 上記の座標系は SoundObject の座標系とは異なる．

1.1 厳密解

上記の問題の厳密解は既知である [1]．平面波の音場 p_i は以下で与えられる．ここで P_n はルジャンドル多項式，j_n は球ベッセル関数である．

$\begin{matrix} (1) & p_{i} = \sum_{n = 0}^{\infty} j^{n} (2 n + 1) P_{n} (\cos θ_{o}) j_{n} (k r) \end{matrix}$

また，散乱波の音場 p_r は以下で与えられる．ここで h_n⁽²⁾ は球ハンケル関数である．

$\begin{matrix} (2) & p_{r} = - \sum_{n = 0}^{\infty} j^{n} (2 n + 1) P_{n} (\cos θ_{o}) j_{n}^{'} (k a) \frac{h_{n}^{(2)} (k r)}{h_{n}^{(2)'} (k a)} \end{matrix}$

従って，球に入射する平面波の音圧と，球の表面で観測される音圧の比を表す周波数伝達関数 G (jω) は以下で与えられる．

$\begin{matrix} (3) & G (j ω) = {\frac{p_{i} + p_{r}}{p_{i}}|}_{r = a} \end{matrix}$

1.2 既存の近似解

上記の厳密解は計算可能であるが非常に煩雑であるため，近似解が提案されている．[1], [2] には，ka ≪ 1 となる場合の散乱波の近似解が示されている．しかし，球による頭部の近似では，ka = 1 となる周波数は約 760Hz となる．このためこれらは今回の用途には実用的ではない．更に，[2] には，kr ≪ 1 となる場合の 2 重音源 (ダイポール音源) による散乱波の近似解が示されているが，これも適用が困難である．そこで，本ドキュメントでは 2 重音源による散乱波の更なる近似を提案する．

1.3 提案する近似解

Φ_i を観測位置 (r, θ₀) における平面波の速度ポテンシャルとする．Φ_i は以下で与えられる．ここで A は未定係数である．

$\begin{matrix} (4) & Φ_{i} = A e^{j (ω t + k x)} = A e^{j (ω t + k r \cos θ_{o})} \end{matrix}$

原点における 2 重音源によって散乱波を近似する．Φ_rを観測位置 (r, θ₀) における速度ポテンシャルとする．Φ_r は以下の式で与えられる．ここで，B も未定係数である．

$\begin{matrix} (5) & Φ_{r} = \frac{B \cos θ_{o}}{r^{2}} (1 + j k r) e^{j (ω t - k r)} \end{matrix}$

従って，球の近傍の速度ポテンシャル Φ は以下となる．

$\begin{matrix} (6) & \begin{matrix} \begin{array}{r} Φ \end{array} \begin{array}{l} = Φ_{i} + Φ_{r} \\ = \{A e^{j k r \cos θ_{o}} + \frac{B \cos θ_{o}}{r^{2}} (1 + j k r) e^{- j k r}\} e^{j ω t} \end{array} \end{matrix} \end{matrix}$

粒子速度を求めるために，上記の式を法線微分する．

$\begin{matrix} (7) & \begin{matrix} \begin{array}{r} \frac{\partial Φ}{\partial r} \end{array} \begin{array}{l} = [j k A \cos θ_{o} e^{j k r \cos θ_{o}} - B \cos θ_{o} \{\frac{1}{r^{3}} (2 + j k r) e^{- j k r} + \frac{j k r}{r^{3}} (1 + j k r) e^{- j k r}\}] e^{j ω t} \\ = [j k A \cos θ_{o} e^{j k r \cos θ_{o}} - \frac{B \cos θ_{o}}{r^{3}} \{{(j k r)}^{2} + j 2 k r + 2\} e^{- j k r}] e^{j ω t} \end{array} \end{matrix} \end{matrix}$

粒子速度は r = a で 0 となる．

$\begin{matrix} (8) & \begin{matrix} {\frac{\partial Φ}{\partial r}|}_{r = a} = 0 \\ ∴ B = \frac{j k a^{3} A e^{j k a \cos θ_{o}}}{\{{(j k a)}^{2} + j 2 k a + 2\} e^{- j k a}} \end{matrix} \end{matrix}$

よって，球近傍の速度ポテンシャル Φ は，以下で与えられる．

$\begin{matrix} (9) & Φ = \{A e^{j k r \cos θ_{o}} + \frac{j k a^{3} A e^{j k a \cos θ_{o}}}{\{{(j k a)}^{2} + j 2 k a + 2\} e^{- j k a}} \frac{\cos θ_{o}}{r^{2}} (1 + j k r) e^{- j k r}\} e^{j ω t} \end{matrix}$

以上より，球の表面における速度ポテンシャルは以下で与えられる．

$\begin{matrix} (10) & {Φ|}_{r = a} = A e^{j (ω t + k a \cos θ_{o})} \{1 + \frac{j k a (1 + j k a) \cos θ_{o}}{{(j k a)}^{2} + j 2 k a + 2}\} \end{matrix}$

2. 球散乱効果の伝達関数

以上より，平面波の音圧に対する球の表面で観測される音圧の比を示す周波数伝達関数 G (jω) は以下で与えられる．

$\begin{matrix} (11) & \begin{matrix} \begin{array}{r} G (j ω) \end{array} \begin{array}{l} = {\frac{ρ \frac{\partial Φ}{\partial t}}{ρ \frac{\partial Φ_{i}}{\partial t}}|}_{r = a} = {\frac{j ω Φ}{{j ω Φ}_{i}}|}_{r = a} \\ = 1 + \frac{j k a (1 + j k a) \cos θ_{o}}{{(j k a)}^{2} + j 2 k a + 2} \\ = 1 + \frac{{(j a ω)}^{2} + j a c ω}{{(j a ω)}^{2} + j 2 a c ω + 2 c^{2}} \cos θ_{o} \end{array} \end{matrix} \end{matrix}$

ここで，ω_c = c /a とすると上記の周波数伝達関数 G (jω) に対応する伝達関数 G (s) は以下で与えられる．

$\begin{matrix} (12) & \begin{matrix} \begin{array}{r} G (s) \end{array} \begin{array}{l} = 1 + \frac{a^{2} s^{2} + a c s}{a^{2} s^{2} + 2 a c s + 2 c^{2}} \cos θ_{o} \\ = 1 + \cos θ_{o} - \frac{ω_{c} (s + 2 ω_{c}) \cos θ_{o}}{s^{2} + 2 ω_{c} s + 2 {ω_{c}}^{2}} \end{array} \end{matrix} \end{matrix}$

G (jω) の周波数特性の例を以下に示す．ここで，c = 343.7 m/s, a = 71.5 mm である．

f:id:suzumushi0:20210807160042p:plain — **Fig. 2: An example of frequency characteristics of scattering effect by a sphere.**

また，周波数伝達関数 G (jω) の指向特性の例も以下に示す．半径方向がゲイン (ratio) を，x 軸からの角度が θ_o を示す．球の直径を波長とする周波数は約 2,400 Hz となる．2,000 Hz 以下では球の後方への入射波の伝搬が顕著となるが，2,000 Hz を超えると正面方向のゲインに差は殆どなく，更に 3,000 Hz を越えると指向特性に差がなくなる事が図に示されている．

f:id:suzumushi0:20211027192258p:plain — **Fig. 3: An example of directional characteristics of scattering effect by a sphere.**

参考に，式 (3) を数値計算した厳密解による周波数伝達関数の指向特性の例を以下に示す．厳密解と近似解の指向特性は，細部において差異があるものの，傾向的には同じである．頭部は厳密な剛体球では無いため，提案した近似解で十分な効果が期待できる．

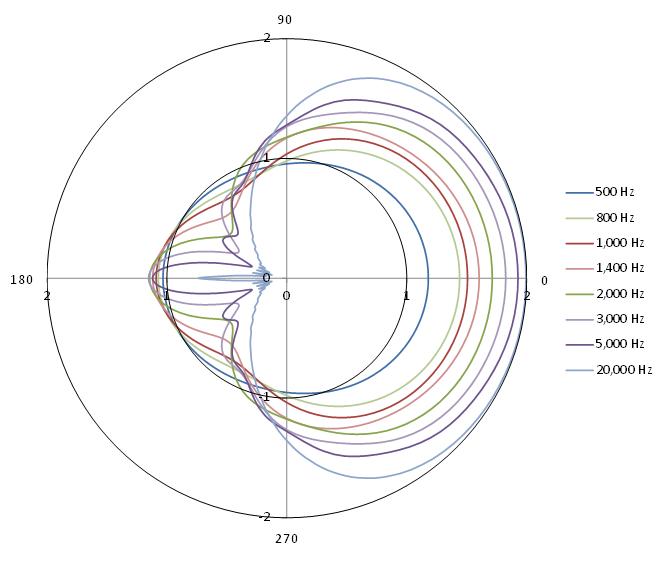
f:id:suzumushi0:20211027192326p:plain — **Fig. 4: An example of directional characteristics based on the exact solution.**

Note: 厳密解の数値計算プログラムは以下のリンクにある．

github.com

3. 球散乱効果フィルタ

式 (12) の伝達関数 G (s) と等価なシステム伝達関数 H (z) を実現する IIR フィルタを双一次変換によって求める．双一次変換による IIR フィルタの設計方法は既知であるため説明は省略する．必要であれば以下を参照せよ．

suzumushi0.hatenablog.com

双一次変換により伝達関数 G (s) とシステム伝達関数 H (z) の角周波数の対応関係に歪が生じる．このため，ω_cに対応する補正された角周波数 ω_a を以下に示す．ここで T はサンプリング周期である．

$\begin{matrix} (13) & ω_{a} = \tan (\frac{ω_{c} T}{2}) = \tan (\frac{c T}{2 a}) \end{matrix}$

従ってシステム伝達関数 H (z) は以下で与えられる．

$\begin{matrix} (14) & \begin{array}{l} H (z) = {G (s)|}_{s = \frac{1 - z^{- 1}}{1 + z^{- 1}}, ω_{c} = ω_{a}} \\ = 1 + \cos θ_{o} - \frac{ω_{a} (\frac{1 - z^{- 1}}{1 + z^{- 1}} + 2 ω_{a}) \cos θ_{o}}{{(\frac{1 - z^{- 1}}{1 + z^{- 1}})}^{2} + 2 ω_{a} \frac{1 - z^{- 1}}{1 + z^{- 1}} + 2 {ω_{a}}^{2}} \\ = 1 + \cos θ_{o} - \frac{ω_{a} \{(2 ω_{a} + 1) + 4 ω_{a} z^{- 1} + (2 ω_{a} - 1) z^{- 2}\} \cos θ_{o}}{(2 {ω_{a}}^{2} + 2 ω_{a} + 1) + 2 (2 {ω_{a}}^{2} - 1) z^{- 1} + (2 {ω_{a}}^{2} - 2 ω_{a} + 1) z^{- 2}} \\ = 1 + \frac{\{(ω_{a} + 1) - 2 z^{- 1} - (ω_{a} - 1) z^{- 2}\} \cos θ_{o}}{(2 {ω_{a}}^{2} + 2 ω_{a} + 1) + 2 (2 {ω_{a}}^{2} - 1) z^{- 1} + (2 {ω_{a}}^{2} - 2 ω_{a} + 1) z^{- 2}} \end{array} \end{matrix}$

上記は，本質的に 2 次の IIR フィルタ (双 2 次フィルタ) で実装できる．上記のディジタルフィルタの周波数特性の例を以下に示す．ここで T = 1 /44,100 sとしている．

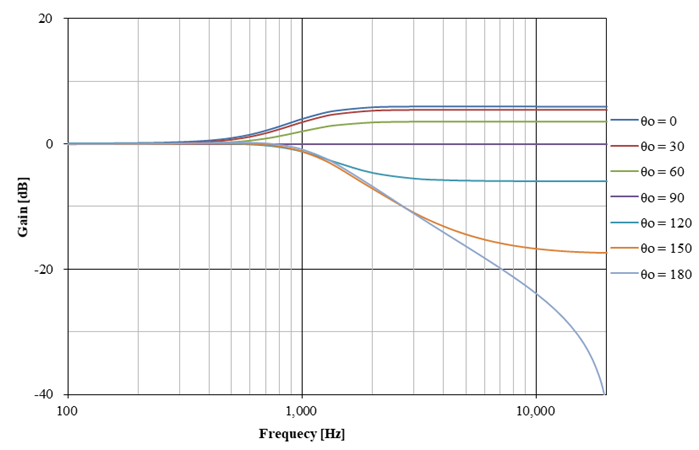
f:id:suzumushi0:20210807161050p:plain — **Fig. 5: An example of frequency characteristics of sphere scattering effect filter.**

4. 評　　価

SoundObject では，球による散乱波 (Scattered waves by sphere)，両耳間時間差，レベル差を伴った入射波 (Incident wave /w ITD and ILD) から出力を選択できる．従って，これらの出力の比較により球散乱効果フィルタの評価ができる．以下のビデオに示す通り，両耳間時間差，レベル差を伴った入射波では，距離に係わらず耳元に音源がある様に思える．一方，球による散乱波では，球散乱効果フィルタにより明確な距離感が得られる事が判る．

www.youtube.com