1. 正弦波のベクトル表示 - 趣味人のブログ

本章では，先ず1.1において，正弦波のベクトル表示の定義を述べる．次に1.2 において，正弦波は，これと角周波数が等しい正弦波に分解でき，これら正弦波のベクトル表示の間には，ベクトルの分解や合成の関係が成立する事を示す．そして 1.3 において，角周波数が等しい正弦波の合成は，これらの正弦波のベクトル表示から容易に求められる事を示す．

1.1. 正弦波のベクトル表示の定義
1.2. 正弦波の分解とベクトル表示の関係
1.3. 角周波数が等しい正弦波の合成
- 三角関数による合成
- 静止ベクトルによる合成

1.1. 正弦波のベクトル表示の定義

固定された観測点において，時間 t に観測された変位 y (t) が以下の式で表される振動を正弦波と言う．

$\begin{matrix} (1-1) & y (t) = A s i n (ω t + φ) \end{matrix}$

ここで A は振幅 (変位の最大値)，ω は角周波数 (角振動数，円振動数とも呼ばれる)，φ は初期位相，(ωt + φ) は位相と呼ばれる．正弦波の時間変化を図1‑1 に示す．

f:id:suzumushi0:20170604143536p:plain — **図1-1: 正弦波の時間変化．**

Note: 分野や文献によっては，正弦波を x (t) = A cos (ωt + φ) と定義する場合もある．

Note: 分野や文献 (特に通信工学) によっては，式 (1‑1) の φ を位相と呼ぶ場合がある．文献を読む際に，位相の定義を確認，若しくは文脈から読み取る必要がある．

直交座標における正弦波の変位 y (t)，振幅 A，位相 (ωt + φ) の関係を，以下の図に示す．ここで，偏角 (ωt + φ) の動径と，原点 O を中心とする半径 A の円の交点を P (t) とする．P (t) は時間 t の経過と共に反時計回りに角周波数 ω で回転する．

f:id:suzumushi0:20170604143537p:plain — **図1-2: 正弦波の変位，振幅，位相の関係 (回転ベクトル)．**

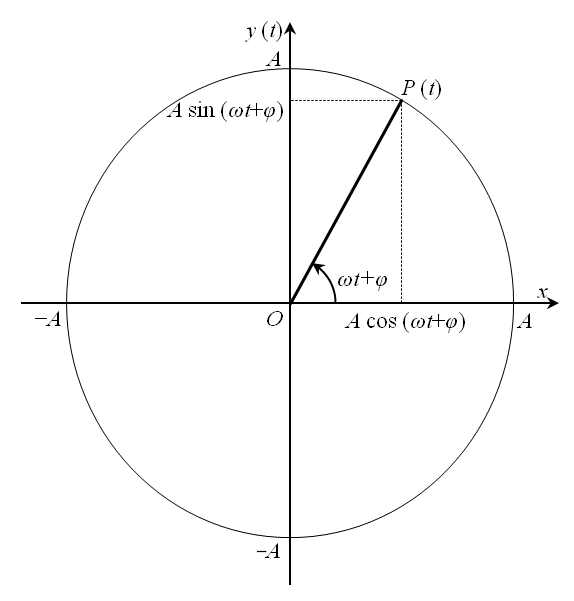
P (t) の座標を成分の組とするベクトルは，正弦波の回転ベクトルと呼ばれ，以下の式で与えられる．

$\begin{matrix} (1-2) & P (t) = (A c o s (ω t + φ), A s i n (ω t + φ)) \end{matrix}$

図から明らかな通り，P (t) は，振幅 A を絶対値，位相 (ωt + φ) を偏角とする極座標を，直交座標に変換したものである．

また，時間 t = 0 の際の変位，振幅，位相の関係を図1‑3に示す．P (0) は正弦波の静止ベクトルと呼ばれ，以下の式で与えられる．

$\begin{matrix} (1-3) & P (0) = (A c o s φ, A s i n φ) \end{matrix}$

f:id:suzumushi0:20170604143538p:plain — **図1-3: 時間 t = 0 における正弦波の変位，振幅，位相の関係 (静止ベクトル)．**

図から明らかな通り，P (0) の座標は，振幅 A を絶対値，初期位相 φ を偏角とする極座標を，直交座標に変換したものである．

Note: 上記の振幅を交流の実効値に置き換えると，電気工学における静止ベクトル表示となる．

1.2. 正弦波の分解とベクトル表示の関係

次に，正弦波は，これと角周波数が等しい正弦波に分解でき，これら正弦波のベクトル表示の間には，ベクトルの分解や合成の関係が成立する事を示す．高校数学で学習した三角関数の加法定理により，式 (1‑1) に示した正弦波は，以下の通り位相が直交する (位相差がπ / 2 となる) 正弦波に分解できる．

$\begin{matrix} (1-4) & \begin{matrix} \begin{array}{r} y (t) \end{array} \begin{array}{l} = A s i n (ω t + φ) \\ = A c o s φ s i n (ω t) + A s i n φ c o s (ω t) \\ = A c o s φ s i n (ω t) + A s i n φ s i n (ω t + \frac{π}{2}) \end{array} \end{matrix} \end{matrix}$

式 (1‑4) から明らかな様に，分解された正弦波の角周波数は元の正弦波の角周波数と等しい．また振幅が |A cos φ|，初期位相が 0 の正弦波と，振幅が |A sin φ|，初期位相が π / 2 の正弦波に分解できる．当然，逆の関係も成立し，これらの正弦波から元の正弦波を合成できる．即ち，角周波数が等しく，位相が直交する正弦波に適切な振幅を与えれば，これらと角周波数が等しく，任意の振幅と初期位相の正弦波を合成できる．

Note: 余弦波という用語は一般には用いられていないため，初期位相が 0 の余弦関数で表示される正弦波を，初期位相が π / 2 の正弦波と記す．

ここで，元の正弦波の回転ベクトルを P (t)，分解された正弦波の回転ベクトルを各々 P_r(t), P_b(t)とし，これらの成分を以下に示す．また，これらの回転ベクトルの関係を図1‑4に示す．

$\begin{matrix} (1-5) & \begin{matrix} \begin{array}{r} P (t) \end{array} \begin{array}{l} = (A c o s (ω t + φ), A s i n (ω t + φ)) \\ = (A \cos φ c o s (ω t) - A \sin φ s i n (ω t), A \cos φ s i n (ω t) + A \sin φ c o s (ω t)) \end{array} \end{matrix} \end{matrix}$ $\begin{matrix} (1-6) & P_{r} (t) = (A \cos φ c o s (ω t), A \cos φ s i n (ω t)) \end{matrix}$ $\begin{matrix} (1-7) & \begin{matrix} \begin{array}{r} P_{b} (t) \end{array} \begin{array}{l} = (A s i n φ c o s (ω t + \frac{π}{2}), A s i n φ s i n (ω t + \frac{π}{2})) \\ = (- A s i n φ s i n (ω t), A s i n φ c o s (ω t)) \end{array} \end{matrix} \end{matrix}$

f:id:suzumushi0:20170604143539p:plain — **図1-4: 正弦波の分解 (回転ベクトル表示)．**

上記か明らかな通り，これら正弦波の回転ベクトルの間には以下の関係が成立する．

$\begin{matrix} (1-8) & P (t) = P_{r} (t) + P_{b} (t) \end{matrix}$

即ち，正弦波は，これと角周波数が等しく，かつ位相が直交する正弦波に分解でき，その逆の関係も成立する．また，元の正弦波と分解された正弦波の回転ベクトルの間には，ベクトルの分解や合成の関係が成立する．

次に，時間 t = 0 の際のこれらの正弦波の静止ベクトルの成分を以下に示す．また，これらの静止ベクトルの関係を図1‑5に示す．

$\begin{matrix} (1-9) & P (0) = (A \cos φ, A \sin φ) \end{matrix}$ $\begin{matrix} (1-10) & P_{r} (0) = (A \cos φ, 0) \end{matrix}$ $\begin{matrix} (1-11) & P_{b} (0) = (0, A s i n φ) \end{matrix}$

f:id:suzumushi0:20170604143540p:plain — **図1-5: 正弦波の分解 (静止ベクトル表示)．**

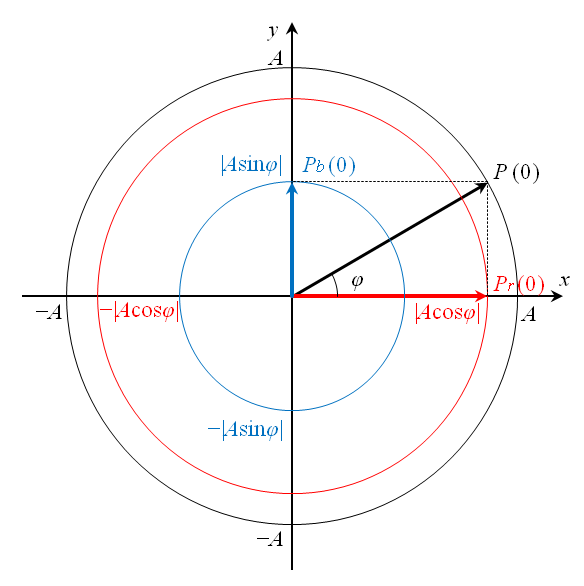
図から明らかな通り，静止ベクトル表示では，分解された正弦波の静止ベクトルは，単純に元の静止ベクトルを直交座標の各座標軸上へ正射影したベクトルとなる．即ち，元の静止ベクトルの各成分の絶対値は，分解された正弦波の振幅を示す．

1.3. 角周波数が等しい正弦波の合成

最後に，角周波数が等しい正弦波の合成 (一次結合，線形結合) は，これらの正弦波のベクトル表示から容易に求められる事を示す．ここで，以下の正弦波の合成を考える．

$\begin{matrix} (1-12) & \begin{matrix} \begin{matrix} {y_{1} (t) = A}_{1} \sin (ω t + φ_{1}) \\ {y_{2} (t) = A}_{2} \sin (ω t + φ_{2}) \end{matrix} \end{matrix} \end{matrix}$

三角関数による合成

先ずベクトル表示を使用せず，三角関数によって正弦波を合成する．式 (1‑13) から明らかな通り，角周波数が等しい正弦波の合成は，これらと同じ角周波数の正弦波となる．

$\begin{matrix} (1-13) & \begin{matrix} \begin{array}{l} y_{1} (t) + y_{2} (t) \\ = A_{1} \sin (ω t + φ_{1}) + A_{2} \sin (ω t + φ_{2}) \\ = A_{1} \cos φ_{1} \sin (ω t) + A_{1} \sin φ_{1} \cos (ω t) + A_{2} \cos φ_{2} \sin (ω t) + A_{2} \sin φ_{2} \cos (ω t) \\ = (A_{1} c o s φ_{1} + A_{2} c o s φ_{2}) \sin (ω t) + (A_{1} s i n φ_{1} + A_{2} s i n φ_{2}) \cos (ω t) \\ = \sqrt{{(A_{1} c o s φ_{1} + A_{2} c o s φ_{2})}^{2} + {(A_{1} s i n φ_{1} + A_{2} s i n φ_{2})}^{2}} \sin (ω t + \tan^{- 1} \frac{A_{1} s i n φ_{1} + A_{2} s i n φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}) \\ = \sqrt{{A_{1}}^{2} + {A_{2}}^{2} + 2 A_{1} A_{2} (c o s φ_{1} c o s φ_{2} + s i n φ_{1} s i n φ_{2})} \sin (ω t + \tan^{- 1} \frac{A_{1} s i n φ_{1} + A_{2} s i n φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}) \\ = \sqrt{{A_{1}}^{2} + {A_{2}}^{2} + 2 A_{1} A_{2} \cos (φ_{1} - φ_{2})} \sin (ω t + \tan^{- 1} \frac{A_{1} s i n φ_{1} + A_{2} s i n φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}}) \end{array} \end{matrix} \end{matrix}$

上記の式は煩雑であるが，最初に個々の正弦波を加法定理によって分解し，次に sin (ωt), cos (ωt) の項に整理してから，高校数学で学習した下記の三角関数の合成定理を適用している展開を理解する事が重要である．

$\begin{matrix} (1-14) & a s i n θ + b c o s θ = \sqrt{a^{2} + b^{2}} \sin (θ + \tan^{- 1} \frac{b}{a}) \end{matrix}$

Note: 上記は，角周波数が等しい正弦波から，これらと角周波数が異なる正弦波を合成出来ない事も示している．

静止ベクトルによる合成

上から明らか通り，角周波数が等しい正弦波の合成は，これと同じ角周波数の正弦波となるため，これらの回転ベクトルの相対的な位置関係は時間 t に依存しない．従って，時間 t = 0 の静止ベクトル表示におけるベクトルの位置関係の考察は，他の時間においても同様に適用できる．そこで，正弦波 y₁(t), y₂(t) の静止ベクトルを各々 P₁, P₂ とすると，これらは以下で与えられる．

$\begin{matrix} (1-15) & \begin{matrix} \begin{matrix} P_{1} = (A_{1} c o s φ_{1}, A_{1} \sin φ_{1}) \\ P_{2} = (A_{2} c o s φ_{2}, A_{2} \sin φ_{2}) \end{matrix} \end{matrix} \end{matrix}$

1.2 に述べた通り，正弦波 y₁(t) は角周波数が ω，初期位相が 0，振幅が |A₁ cos φ₁| となる正弦波と，角周波数が ω，初期位相が π / 2，振幅が |A₁ sin φ₁| となる正弦波に分解できる．正弦波 y₂(t) も同様である．上記の静止ベクトルの成分の絶対値は，これらの振幅を示している．

ここで，正弦波 y₁(t), y₂(t) から分解された，角周波数が ω，初期位相が 0 となる正弦波同士を合成すると，角周波数，初期位相は元の正弦波に等しく，振幅が単純に |A₁ cos φ₁+ A₂ cos φ₂| となる正弦波となる事は明らかである．初期位相が π / 2となる正弦波の合成の場合も同様に振幅が |A₁ sin φ₁+ A₂ sin φ₂| となる正弦波となる．

よって，正弦波 y₁(t), y₂(t) を合成した正弦波の静止ベクトルは，以下で与えられる．

$\begin{matrix} (1-16) & P_{1} + P_{2} = (A_{1} c o s φ_{1} + A_{2} c o s φ_{2}, A_{1} s i n φ_{1} + A_{2} s i n φ_{2}) \end{matrix}$

以上の，静止ベクトルによる合成前の正弦波と合成された正弦波の関係を図1-6に示す．赤線と青線は合成前の正弦波，黒線は合成された正弦波の静止ベクトルを表す．

f:id:suzumushi0:20170604143541p:plain — **図1-6: 静止ベクトルによる正弦波の合成．**

従って，正弦波 y₁(t), y₂(t) を合成した正弦波の角周波数は ω となる．また，1.1 に述べた通り，静止ベクトルとは振幅を絶対値，初期位相を偏角とする極座標を，直交座標で表示したものであるから，振幅 A，初期位相 φ は以下の式で与えられる．

$\begin{matrix} (1-17) & \begin{matrix} \begin{array}{r} A \end{array} \begin{array}{l} = \sqrt{{(A_{1} c o s φ_{1} + A_{2} c o s φ_{2})}^{2} + {(A_{1} s i n φ_{1} + A_{2} s i n φ_{2})}^{2}} \\ = \sqrt{{A_{1}}^{2} + {A_{2}}^{2} + 2 A_{1} A_{2} (c o s φ_{1} c o s φ_{2} + s i n φ_{1} s i n φ_{2})} \\ = \sqrt{{A_{1}}^{2} + {A_{2}}^{2} + 2 A_{1} A_{2} \cos (φ_{1} - φ_{2})} \end{array} \end{matrix} \end{matrix}$ $\begin{matrix} (1-18) & φ = \tan^{- 1} \frac{A_{1} s i n φ_{1} + A_{2} s i n φ_{2}}{A_{1} c o s φ_{1} + A_{2} c o s φ_{2}} \end{matrix}$

これらの結果は三角関数による合成と一致する．以上より，角周波数が等しい正弦波の合成は，これらの静止ベクトル表示から容易に求める事が出来る．尚，この計算方法の適用範囲はあくまで角周波数が等しい正弦波の合成であり，角周波数が異なる場合に適用できない事は勿論である．