3. 正弦波交流とインピーダンス

本章では，先ず3.1 において正弦波交流の定義を述べる．そして，3.2 以降において，誘導リアクタンス，容量リアクタンス，レジスタンス，及び RLC 直列回路，並列回路における合成インピーダンスを，正弦波交流，及び複素正弦波交流の双方において求め，前者は交流電圧と電流の振幅や実効値の関係を表示しているが，後者は瞬時値の関係を表示している事を示す．尚，正弦波交流に関する部分は全て高校物理で学習した (はずの) 内容である．

3.1. 正弦波交流の定義
3.2. 誘導リアクタンス
- 正弦波交流における誘導リアクタンス
- 複素正弦波交流における誘導リアクタンス
3.3. 容量リアクタンス
- 正弦波交流における容量リアクタンス
- 複素正弦波交流における容量リアクタンス
3.4. レジスタンス
- 正弦波交流におけるレジスタンス
- 複素正弦波交流におけるレジスタンス
3.5. RLC 直列回路における合成インピーダンス
- 正弦波交流における合成インピーダンス
- 複素正弦波交流における複素合成インピーダンス
3.6. RLC 並列回路における合成インピーダンス
- 正弦波交流における合成インピーダンス
- 複素正弦波交流における複素合成インピーダンス
余談: 交流のフェーザ表示

3.1. 正弦波交流の定義

時間 t に観測された電圧の瞬時値 V (t) [V] が以下の式で表される電圧の振動を正弦波交流電圧と言う．

$\begin{matrix} (3-1) & V (t) = V_{a} s i n (ω t + φ) \end{matrix}$

ここで V_a [V] は正弦波交流電圧の振幅 (最大値)，ω [rad/s] は角周波数，φ [rad] は初期位相，(ωt + φ) [rad] は位相と呼ばれる．

また，正弦波交流電圧の振幅と時間 t における位相の瞬時値を表示した，複素正弦波交流電圧 v (t) [V] を以下の式に示す．

$\begin{matrix} (3-2) & v (t) = V_{a} e^{j (ω t + φ)} = V_{a} e^{j φ} e^{j ω t} \end{matrix}$

2.2 に述べた通り，この場合の電圧の瞬時値 V (t) [V] は以下の式で与えられる．

$\begin{matrix} (3-3) & V (t) = I m \{v (t)\} \end{matrix}$

同様に，時間 t に観測された電流の瞬時値 I (t) [A] が以下の式で表される電流の振動を正弦波交流電流と言う．ここで I_a [A] は正弦波交流電流の振幅 (最大値) を示す．

$\begin{matrix} (3-4) & I (t) = I_{a} s i n (ω t + φ) \end{matrix}$

また，正弦波交流電流の振幅と時間 t における位相の瞬時値を表示した，複素正弦波交流電流 i (t) [A] を以下の式に示す．

$\begin{matrix} (3-5) & i (t) = I_{a} e^{j (ω t + φ)} = I_{a} e^{j φ} e^{j ω t} \end{matrix}$

この場合の電流の瞬時値 I (t) [A] は以下の式で与えられる．

$\begin{matrix} (3-6) & I (t) = I m \{i (t)\} \end{matrix}$

尚，正弦波交流電圧，電流の振幅 (最大値) と実効値 V_e [V], I_e [A] の間には以下の関係がある．

$\begin{matrix} (3-7) & \begin{matrix} \begin{matrix} V_{a} = \sqrt{2} V_{e} \\ I_{a} = \sqrt{2} I_{e} \end{matrix} \end{matrix} \end{matrix}$

また，正弦波交流の角周波数と周波数 f [Hz]，周期 T [s] の間には以下の関係がある．

$\begin{matrix} (3-8) & \begin{matrix} \begin{matrix} ω = 2 π f \\ f = \frac{1}{T} \end{matrix} \end{matrix} \end{matrix}$

3.2. 誘導リアクタンス

インダクタンスが L [H] のコイルに加わる電圧の瞬時値 V (t) [V] と流れる電流の瞬時値 I (t) [A] の間には以下の関係がある．

$\begin{matrix} (3-9) & V (t) = L \frac{d}{d t} I (t) \end{matrix}$

正弦波交流における誘導リアクタンス

コイルに流れる電流を，振幅 I_a [A]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電流とする．ここではコイルに流れる電流と電圧の位相差を求めるため電流の初期位相を 0 としている．この場合，コイルに流れる電流の瞬時値 I (t) [A] は以下となる．

$\begin{matrix} (3-10) & I (t) = I_{a} s i n (ω t) \end{matrix}$

よって，コイルに加わる電圧の瞬時値 V (t) [V] は以下で与えられる．

$\begin{matrix} (3-11) & \begin{matrix} \begin{array}{r} V (t) \end{array} \begin{array}{l} = L \frac{d}{d t} I (t) \\ = L \frac{d}{d t} I_{a} s i n (ω t) \\ = ω L I_{a} c o s (ω t) \\ = ω L I_{a} s i n (ω t + \frac{π}{2}) \end{array} \end{matrix} \end{matrix}$

従って，これらの交流電圧と電流の角周波数は等しく，電圧の位相は電流の位相より π / 2 [rad] 進む．ここで，これらの交流電圧と電流の振幅の比 (実効値の比としても同じ) を，正弦波交流における誘導リアクタンス X_L [Ω] とする．コイルに加わる交流電圧の振幅を V_a [V] とすると X_L [Ω] は以下で与えられる．

$\begin{matrix} (3-12) & X_{L} = \frac{V_{a}}{I_{a}} = \frac{ω L I_{a}}{I_{a}} = ω L \end{matrix}$

Note: 上記の教科書的説明は如何にも苦しい．交流電圧と電流が最大値 (もしくは実効値) となる時間 t は異なるため，これらを時間関数で表示した数式によって説明する事は土台に無理がある．このため，上記の如く捩子くれた様な理論の流れとなるのである．

複素正弦波交流における誘導リアクタンス

コイルに流れる電流を，振幅 I_a [A]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電流とする．この場合，コイルに流れる電流の位相の瞬時値と振幅を表示した，電流の複素数表示 i (t) [A] は以下となる．

$\begin{matrix} (3-13) & i (t) = I_{a} e^{j ω t} \end{matrix}$

よって，コイルに加わる電圧の複素数表示 v (t) [V] は以下で与えられる．

$\begin{matrix} (3-14) & \begin{matrix} \begin{array}{r} v (t) \end{array} \begin{array}{l} = L \frac{d}{d t} i (t) \\ = L \frac{d}{d t} I_{a} e^{j ω t} \\ = j ω L I_{a} e^{j ω t} \end{array} \end{matrix} \end{matrix}$

従って，これらの交流電圧と電流の角周波数は等しい．ここで，これらの交流電圧と電流の複素数表示の比を，複素正弦波交流における誘導リアクタンス Z_L [Ω] とする．Z_L [Ω] は以下で与えられる．

$\begin{matrix} (3-15) & Z_{L} = \frac{v (t)}{i (t)} = \frac{j ω L I_{a} e^{j ω t}}{I_{a} e^{j ω t}} = j ω L \end{matrix}$

2.2 に述べた通り，極形式による正弦波の複素数表示において，絶対値は振幅，偏角は位相を示す．よって，上記の複素正弦波交流における誘導リアクタンスの ωL は交流電圧と電流の振幅の比を，また 2.3に述べた通り，j は交流電圧の位相が電流の位相より π / 2 [rad] 進む事を表示している．即ち，上記の誘導リアクタンスは，コイルに加わる電圧の複素数表示 v (t) [V] と，コイルを流れる電流の複素数表示 i (t) [A] の瞬時値の関係を表示している．

Note: 高校物理で学習した正弦波交流におけるリアクタンスは，交流電圧と電流の振幅や実効値の比を表示するだけで，位相差に関しては言葉によって補われているのみである．従って，複素正弦波交流におけるリアクタンスの方が交流電圧，電流の関係をより正確に表示しているし，その導出過程も理論的となる．

3.3. 容量リアクタンス

キャパシタンスが C [F] のコンデンサに流れる電流の瞬時値 I (t) [A] と加わる電圧の瞬時値 V (t) [V] の間には以下の関係がある．

$\begin{matrix} (3-16) & I (t) = C \frac{d}{d t} V (t) \end{matrix}$

正弦波交流における容量リアクタンス

コンデンサに加わる電圧を，振幅 V_a [V]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電圧とする．ここではコンデンサに加わる電圧と電流の位相差を求めるため電圧の初期位相を 0 としている．この場合，コンデンサに加わる電圧の瞬時値 V (t) [V] は以下となる．

$\begin{matrix} (3-17) & V (t) = V_{a} s i n (ω t) \end{matrix}$

よって，コンデンサに流れる電流の瞬時値 I (t) [A] は以下で与えられる．

$\begin{matrix} (3-18) & \begin{matrix} \begin{array}{r} I (t) \end{array} \begin{array}{l} = C \frac{d}{d t} V (t) \\ = C \frac{d}{d t} V_{a} s i n (ω t) \\ = ω C V_{a} c o s (ω t) \\ = ω C V_{a} s i n (ω t + \frac{π}{2}) \end{array} \end{matrix} \end{matrix}$

従って，これらの交流電圧と電流の角周波数は等しく，電流の位相は電圧の位相より π / 2 [rad] 進む．ここで，これらの交流電圧と電流の振幅の比 (実効値の比としても同じ) を，正弦波交流における容量リアクタンス X_C [Ω] とする．コンデンサに流れる交流電流の振幅を I_a [A] とすると X_C [Ω] は以下で与えられる．

$\begin{matrix} (3-19) & X_{C} = \frac{V_{a}}{I_{a}} = \frac{V_{a}}{ω C V_{a}} = \frac{1}{ω C} \end{matrix}$

複素正弦波交流における容量リアクタンス

コンデンサに加わる電圧を，振幅 V_a [V]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電圧とする．この場合，コンデンサに加わる電圧の位相の瞬時値と振幅を表示した，電圧の複素数表示 v (t) [V] は以下となる．

$\begin{matrix} (3-20) & v (t) = V_{a} e^{j ω t} \end{matrix}$

よって，コンデンサに流れる電流の複素数表示 i (t) [V] は以下で与えられる．

$\begin{matrix} (3-21) & \begin{matrix} \begin{array}{r} i (t) \end{array} \begin{array}{l} = C \frac{d}{d t} v (t) \\ = C \frac{d}{d t} V_{a} e^{j ω t} \\ = j ω C V_{a} e^{j ω t} \end{array} \end{matrix} \end{matrix}$

従って，これらの交流電圧と電流の角周波数は等しい．ここで，これらの交流電圧と電流の複素数表示の比を，複素正弦波交流における容量リアクタンス Z_C [Ω] とする．Z_C [Ω] は以下で与えられる．

$\begin{matrix} (3-22) & Z_{C} = \frac{v (t)}{i (t)} = \frac{V_{a} e^{j ω t}}{j ω C V_{a} e^{j ω t}} = \frac{1}{j ω C} = \frac{- j}{ω C} \end{matrix}$

3.2 と同様に，上記の複素正弦波交流における容量リアクタンスの 1 / (ωC) は交流電圧と電流の振幅の比を，−j は交流電圧の位相が電流の位相より π / 2 [rad] 遅れる事を表示している．即ち，上記の容量リアクタンスは，コンデンサに加わる電圧の複素数表示 v (t) [V] と，コンデンサを流れる電流の複素数表示 i (t) [A] の瞬時値の関係を表示している．

3.4. レジスタンス

オームの法則は時間に依存しないから，抵抗値が R [Ω] の抵抗に加わる電圧の瞬時値 V (t) [V] と流れる電流の瞬時値 I (t) [A] の間には以下の関係がある．

$\begin{matrix} (3-23) & V (t) = R I (t) \end{matrix}$

正弦波交流におけるレジスタンス

抵抗に流れる電流を，振幅 I_a [A]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電流とする．ここでは抵抗に流れる電流と電圧の位相差を求めるため電流の初期位相を 0 としている．この場合，抵抗に流れる電流の瞬時値 I (t) [A] は以下となる．

$\begin{matrix} (3-24) & I (t) = I_{a} s i n (ω t) \end{matrix}$

よって，抵抗に加わる電圧の瞬時値 V (t) [V] は以下で与えられる．

$\begin{matrix} (3-25) & V (t) = R I (t) = R I_{a} s i n (ω t) \end{matrix}$

従って，これらの交流電圧と電流の角周波数は等しく，また電圧の位相は電流の位相と等しく，電圧と電流の瞬時値の間には直流の場合と同じオームの法則の関係が成立する．

複素正弦波交流におけるレジスタンス

抵抗に流れる電流を，振幅 I_a [A]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電流とする．この場合，抵抗に流れる電流の位相の瞬時値と振幅を表示した，電流の複素数表示 i (t) [A] は以下となる．

$\begin{matrix} (3-26) & i (t) = I_{a} e^{j ω t} \end{matrix}$

よって，抵抗に加わる電圧の複素数表示 v (t) [V] は以下で与えられる．

$\begin{matrix} (3-27) & v (t) = R i (t) = R I_{a} e^{j ω t} \end{matrix}$

従って，これらの交流電圧と電流の角周波数は等しく，また電圧の位相は電流の位相と等しく，電圧と電流の複素数表示の間にはオームの法則の関係が成立する．

3.5. RLC 直列回路における合成インピーダンス

図3‑1の回路図の通り，抵抗値が R [Ω] の抵抗，インダクタンスが L [H] のコイル，及びキャパシタンスが C [F] のコンデンサを直列に接続した際の合成インピーダンスを求める．

f:id:suzumushi0:20170611121524p:plain — **図3-1: RLC 直列回路．**

正弦波交流における合成インピーダンス

キルヒホッフの法則により，上記の回路の抵抗，コイル，コンデンサを流れる電流の瞬時値は等しいから，これを振幅 I_a [A]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電流とする．ここでは回路に流れる電流と電圧の位相差を求めるため電流の初期位相を 0 としている．この場合，回路に流れる電流の瞬時値 I (t) [A] は以下となる．

$\begin{matrix} (3-28) & I (t) = I_{a} s i n (ω t) \end{matrix}$

抵抗，コイル，コンデンサに加わる交流電圧の瞬時値を各々 V_R (t) [V], V_L (t) [V], V_C (t) [V] とすると，3.2, 3.3, 3.4より，これらは以下で与えられる．

$\begin{matrix} (3-29) & \begin{matrix} \begin{matrix} V_{R} (t) = R I_{a} s i n (ω t) \\ V_{L} (t) = ω L I_{a} s i n (ω t + \frac{π}{2}) \\ V_{C} (t) = \frac{1}{ω C} I_{a} s i n (ω t - \frac{π}{2}) \end{matrix} \end{matrix} \end{matrix}$

ここで，これらの電圧の角周波数は等しいため，これら交流電圧の回転ベクトルの相対的な位置関係は時間 t に依存しない．従って，時間 t = 0 の静止ベクトル表示における交流電圧ベクトルの位置関係の考察は，他の時間においても同様に適用できる．そこで，交流電圧 V_R (t), V_L (t), V_C (t) の静止ベクトルを各々 V_R, V_L, V_C とすると，1.3よりこれらは以下で与えられる．

$\begin{matrix} (3-30) & \begin{matrix} \begin{matrix} V_{R} = (R I_{a}, 0) \\ V_{L} = (0, ω L I_{a}) \\ V_{C} = (0, - \frac{1}{ω C} I_{a}) \end{matrix} \end{matrix} \end{matrix}$

従って，回路に加わる交流電圧の瞬時値を V (t) [V] とすると，その静止ベクトル V は以下で与えられる．

$\begin{matrix} (3-31) & {V = V}_{R} + V_{L} + V_{C} = I_{a} (R, ω L - \frac{1}{ω C}) \end{matrix}$

よって，V (t) [V] の振幅 V_a [V]，初期位相 φ [rad] は以下の通りとなる．

$\begin{matrix} (3-32) & \begin{matrix} \begin{matrix} V_{a} = I_{a} \sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}} \\ φ = {t a n}^{- 1} \frac{ω L - \frac{1}{ω C}}{R} \end{matrix} \end{matrix} \end{matrix}$

従って，回路に加わる交流電圧の位相は電流の位相より φ [rad] 進む．また，回路に加わる交流電圧と電流の振幅の比 (実効値の比としても同じ) を，正弦波交流における合成インピーダンス X [Ω] とすると，X [Ω] は以下で与えられる．

$\begin{matrix} (3-33) & X = \frac{V_{a}}{I_{a}} = \sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}} \end{matrix}$

Note: キルヒホッフの法則に関する「試験問題」が，直流の定常状態の回路に対してのみ出題されるため，多くの者がこの法則が定常状態の直流回路でしか成立しないと誤解している．キルヒホッフの法則は時間に依存しないため，直流，交流の瞬時値，定常状態，過渡状態とは無関係に成立する．

複素正弦波交流における複素合成インピーダンス

キルヒホッフの法則により，上記の回路の抵抗，コイル，コンデンサを流れる電流の瞬時値は等しいから，これを振幅 I_a [A]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電流とする．この場合，回路に流れる電流の位相の瞬時値と振幅を表示した，電流の複素数表示 i (t) [A] は以下となる．

$\begin{matrix} (3-34) & i (t) = I_{a} e^{j ω t} \end{matrix}$

抵抗，コイル，コンデンサに加わる交流電圧の複素数表示を各々 v_R (t) [V], v_L (t) [V], v_C (t) [V] とすると，3.2, 3.3, 3.4より，これらは以下で与えられる．

$\begin{matrix} (3-35) & \begin{matrix} \begin{matrix} v_{R} (t) = R I_{a} e^{j ω t} \\ v_{L} (t) = j ω L I_{a} e^{j ω t} \\ v_{C} (t) = \frac{- j}{ω C} I_{a} e^{j ω t} \end{matrix} \end{matrix} \end{matrix}$

従って，回路に加わる交流電圧の複素数表示 v (t) [V] は以下で与えられる．

$\begin{matrix} (3-36) & {v (t) = v}_{R} (t) + v_{L} (t) + v_{C} (t) = \{R + j (ω L - \frac{1}{ω C})\} I_{a} e^{j ω t} \end{matrix}$

ここで，回路に加わる交流電圧と電流の複素数表示の比を，複素正弦波交流における複素合成インピーダンス Z [Ω] とする．Z [Ω] は以下で与えられる．

$\begin{matrix} (3-37) & Z = \frac{v (t)}{i (t)} = \frac{\{R + j (ω L - \frac{1}{ω C})\} I_{a} e^{j ω t}}{I_{a} e^{j ω t}} = R + j (ω L - \frac{1}{ω C}) \end{matrix}$

2.2 に述べた通り，極形式による正弦波の複素数表示において，絶対値は振幅，偏角は位相を示す．よって，上記の複素正弦波交流における複素合成インピーダンスの絶対値は交流電圧と電流の振幅の比を，また 2.3に述べた通り，偏角は交流電流の位相を基準とした交流電圧の位相の進みを表す．これらを以下に示す．

$\begin{matrix} (3-38) & \begin{matrix} \begin{matrix} |Z| = \sqrt{R^{2} + {(ω L - \frac{1}{ω C})}^{2}} \\ A r g (Z) = {t a n}^{- 1} \frac{ω L - \frac{1}{ω C}}{R} \end{matrix} \end{matrix} \end{matrix}$

即ち，上記の合成複素インピーダンスは，回路に加わる電圧の複素数表示 v (t) [V] と，回路を流れる電流の複素数表示 i (t) [A] の瞬時値の関係を表示している．

Note: 複素合成インピーダンスを，正弦波の複素数表示と混同しない事．インピーダンスは正弦波交流電圧と電流の比であり，正弦波では無い．

3.6. RLC 並列回路における合成インピーダンス

図3‑2 の回路図の通り，抵抗値が R [Ω] の抵抗，インダクタンスが L [H] のコイル，及びキャパシタンスが C [F] のコンデンサを並列に接続した際の合成インピーダンスを求める．

f:id:suzumushi0:20170611121525p:plain — **図3-2: RLC 並列回路．**

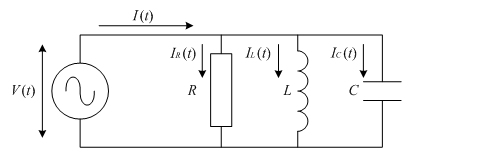
正弦波交流における合成インピーダンス

キルヒホッフの法則により，上記の回路の抵抗，コイル，コンデンサに加わる電圧の瞬時値は等しいから，これを振幅 V_a [V]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電圧とする．ここでは回路に加わる電圧と電流の位相差を求めるため電圧の初期位相を 0 としている．この場合，回路に加わる電圧の瞬時値 V (t) [V] は以下となる．

$\begin{matrix} (3-39) & V (t) = V_{a} s i n (ω t) \end{matrix}$

抵抗，コイル，コンデンサに流れる交流電流の瞬時値を各々 I_R (t) [A], I_L (t) [A], I_C (t) [A] とすると，3.2, 3.3, 3.4より，これらは以下で与えられる．

$\begin{matrix} (3-40) & \begin{matrix} \begin{matrix} I_{R} (t) = \frac{1}{R} V_{a} s i n (ω t) \\ I_{L} (t) = \frac{1}{ω L} V_{a} s i n (ω t - \frac{π}{2}) \\ I_{C} (t) = ω C V_{a} s i n (ω t + \frac{π}{2}) \end{matrix} \end{matrix} \end{matrix}$

ここで，これらの電流の角周波数は等しいため，これら交流電流の回転ベクトルの相対的な位置関係は時間 t に依存しない．従って，時間 t = 0 の静止ベクトル表示における交流電流ベクトルの位置関係の考察は，他の時間においても同様に適用できる．そこで，交流電流 I_R (t), I_L (t), I_C (t) の静止ベクトルを各々 I_R, I_L, I_C とすると，1.3よりこれらは以下で与えられる．

$\begin{matrix} (3-41) & \begin{matrix} \begin{matrix} I_{R} = (\frac{1}{R} V_{a}, 0) \\ I_{L} = (0, - \frac{1}{ω L} V_{a}) \\ I_{C} = (0, ω C V_{a}) \end{matrix} \end{matrix} \end{matrix}$

従って，回路に流れる交流電流の瞬時値を I (t) [A] とすると，その静止ベクトル I は以下で与えられる．

$\begin{matrix} (3-42) & {I = I}_{R} + I_{L} + I_{C} = V_{a} (\frac{1}{R}, ω C - \frac{1}{ω L}) \end{matrix}$

よって，I (t) [A] の振幅 I_a [V]，初期位相 φ [rad] は以下の通りとなる．

$\begin{matrix} (3-43) & \begin{matrix} \begin{matrix} I_{a} = V_{a} \sqrt{\frac{1}{R^{2}} + {(ω C - \frac{1}{ω L})}^{2}} \\ φ = {t a n}^{- 1} \{R (ω C - \frac{1}{ω L})\} \end{matrix} \end{matrix} \end{matrix}$

従って，回路に流れる交流電流の位相は電圧の位相より φ [rad] 進む．また，回路に加わる交流電圧と電流の振幅の比 (実効値の比としても同じ) を，正弦波交流における合成インピーダンス X [Ω] とすると，X [Ω] は以下で与えられる．

$\begin{matrix} (3-44) & X = \frac{V_{a}}{I_{a}} = \frac{1}{\sqrt{\frac{1}{R^{2}} + {(ω C - \frac{1}{ω L})}^{2}}} \end{matrix}$

複素正弦波交流における複素合成インピーダンス

キルヒホッフの法則により，上記の回路の抵抗，コイル，コンデンサに加わる電圧の瞬時値は等しいから，これを振幅 V_a [V]，角周波数 ω [rad/s]，初期位相 0 [rad] の正弦波交流電圧とする．この場合，回路に加わる電圧の位相の瞬時値と振幅を表示した，電圧の複素数表示 v (t) [V] は以下となる．

$\begin{matrix} (3-45) & v (t) = V_{a} e^{j ω t} \end{matrix}$

抵抗，コイル，コンデンサを流れる交流電流の複素数表示を各々 i_R (t) [A], i_L (t) [A], i_C (t) [A] とすると，3.2, 3.3, 3.4より，これらは以下で与えられる．

$\begin{matrix} (3-46) & \begin{matrix} \begin{matrix} i_{R} (t) = \frac{1}{R} V_{a} e^{j ω t} \\ i_{L} (t) = \frac{- j}{ω L} V_{a} e^{j ω t} \\ i_{C} (t) = j ω C V_{a} e^{j ω t} \end{matrix} \end{matrix} \end{matrix}$

従って，回路を流れる交流電流の複素数表示 i (t) [V] は以下で与えられる．

$\begin{matrix} (3-47) & {i (t) = i}_{R} (t) + i_{L} (t) + i_{C} (t) = \{\frac{1}{R} + j (ω C - \frac{1}{ω L})\} V_{a} e^{j ω t} \end{matrix}$

$\begin{matrix} (3-48) & Z = \frac{v (t)}{i (t)} = \frac{V_{a} e^{j ω t}}{\{\frac{1}{R} + j (ω C - \frac{1}{ω L})\} V_{a} e^{j ω t}} = \frac{1}{\frac{1}{R} + j (ω C - \frac{1}{ω L})} \end{matrix}$

$\begin{matrix} (3-49) & \begin{matrix} \begin{matrix} |Z| = \frac{1}{\sqrt{\frac{1}{R^{2}} + {(ω C - \frac{1}{ω L})}^{2}}} \\ A r g (Z) = {t a n}^{- 1} \{R (ω C - \frac{1}{ω L})\} \end{matrix} \end{matrix} \end{matrix}$

余談: 交流のフェーザ表示

本資料では，多くの教科書に記載されている，交流のフェーザ表示によるリアクタンスやインピーダンスの記述方法を意図的に無視している．ここまでの議論，特に式 (3‑15), (3‑22), (3‑37), (3‑48) において交流電圧と電流の角周波数は等しく，これらの比を取った際に e ^jωtが約分され，最終的にはこれが必要無くなる事を十分理解した上で，計算を簡略化する技法として交流のフェーザ表示を利用するのであれば問題ない．

しかし，多くの教科書では，こうした予備知識を説明せず，いきなりフェーザ表示によるリアクタンスやインピーダンスの計算方法を天下り式に提示するため，フェーザ表示では交流の実効値が使用されるのが慣例である事もあり，これが何と何の関係を表示しているのかすら理解出来なくなるのである．電気回路に係る設計では交流の実効値を求めれば良く，瞬時値まで議論する必要は無い場合も多いが，それなら静止ベクトルで計算すれば十分であり，わざわざ複素数表示を使用する必要性は無い．

趣味人のブログ

Cogito, ergo sum. 我思う故に我あり．

3. 正弦波交流とインピーダンス

3.1. 正弦波交流の定義

3.2. 誘導リアクタンス

正弦波交流における誘導リアクタンス

複素正弦波交流における誘導リアクタンス

3.3. 容量リアクタンス

正弦波交流における容量リアクタンス

複素正弦波交流における容量リアクタンス

3.4. レジスタンス

正弦波交流におけるレジスタンス

複素正弦波交流におけるレジスタンス

3.5. RLC 直列回路における合成インピーダンス

正弦波交流における合成インピーダンス

複素正弦波交流における複素合成インピーダンス

3.6. RLC 並列回路における合成インピーダンス

正弦波交流における合成インピーダンス

複素正弦波交流における複素合成インピーダンス

余談: 交流のフェーザ表示