10. ディジタル信号処理の論理モデルと実装モデル

本章は，先ず，10.1において，ディジタル信号処理の理論モデルと実装モデルを述べ，システム伝達関数は，物理的に実存しない想像上の概念であるインパルス列の関係を記述している事を示す．次に，10.2 において，システム伝達関数を実装モデルに適用するために，論理モデルのインパルス列と実装モデルの階段関数の信号との関係に基づいたゲインの補正方法を述べ，10.3において，この方法では誤差が生じる事を示す．このため10.4 及び 10.5において，アナログフィルタとディジタルフィルタにおけるインパルス応答の関係に基づいた，この誤差の補正方法を明らかにする．最後に10.6において 0 次ホールドの伝達関数を示し，ディジタルフィルタの設計には，これも考慮する必要がある事を述べる．

10.1. ディジタル信号処理の論理モデルと実装モデルの関係

ディジタル信号処理の論理モデルと実装モデルを図10-1 に示す．上のブロックダイヤグラムは論理モデルを，下のブロックダイヤグラムは実装モデルを表す．

図10-1: ディジタル信号処理の論理モデルと実装モデル．

ディジタル信号処理の論理モデル

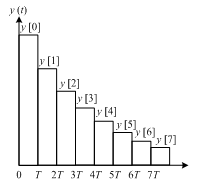
9.2 に述べた通り，ディジタル信号処理の論理モデルでは，サンプラーにおいて，連続時間信号の入力 x (t) はサンプリング周期 T で生成される単位インパルス関数 (櫛型関数) と乗算され，インパルス列 p (t) に変換される．インパルス列 p (t) における各単位インパルス関数の係数は離散時間信号 x [n] となり，ディジタル信号処理の入力となる．

そして，ディジタル信号処理の出力の離散時間信号 y [n] は，再びインパルス列 q (t) と見做され 0 次ホールドに入力される．0 次ホールドはインパルス列 q (t) を階段関数の信号 y (t) に変換して出力する．

ディジタル信号処理の実装モデル

一方，ディジタル信号処理の実装モデルでは，連続時間信号の入力 x (t) は最初に SH (Sample and hold) に入力される．これは，次段の A/D 変換器 (Analog-to-digital converter) が，アナログ入力からディジタル出力への変換に要する時間の間，A/D 変換器の入力を安定化させる目的で設けられている．SH は，次段の A/D 変換器がアナログ入力をディジタル出力に変換する際に，連続時間信号の入力 x (t) をごく短時間保持して A/D 変換器に出力する．尚，これ以外のタイミングにおいて SH は x (t) をそのまま出力する．

A/D 変換器は，サンプリング周期 T 毎に，アナログ入力をディジタル出力 (量子化された離散時間信号 x [n]) に変換する．ディジタル信号処理部分は，論理回路，DSP，コンピュータ等で構成される．D/A 変換器 (Digital-to-analog converter) は，サンプリング周期 T 毎に，ディジタル入力 (量子化された離散時間信号 y [n]) をアナログ出力 (階段関数の信号 y (t)) に変換する．

出力側の SH は，前段の D/A 変換器のディジタル入力が変化する際に生じるノイズを避ける目的で設けられている．多くの場合，D/A 変換器ではディジタル入力の MSB が変化する際に大きなノイズが生じる．このため，SH は前段の D/A 変換器のディジタル入力が変化する際に，出力信号 y (t) をごく短時間保持する．尚，これは簡易な用途では省略される事が多い．

論理モデルと実装モデルの関係

何れのモデルも，連続時間信号の周期的な瞬時値を離散時間信号としている点は同じである．しかし，これらのモデルにおける離散時間信号の意味は全く異なる．論理モデルにおける離散時間信号とは，インパルス列における各単位インパルス関数の係数の事である．一方，実装モデルにおける離散時間信号は，図10-2 に示す様に D/A 変換器の出力が階段関数となる事から，階段関数の信号における各階段の高さを示す係数を意味する．

図10-2: 階段関数の信号．

論理モデルにおけるサンプラーは，連続時間信号の入力 x (t) を，インパルス列 p (t) に変換する．一方，実装モデルにおける SH と A/D 変換器は，連続時間信号の入力 x (t) を離散時間信号 x [n] に変換する．また，論理モデルにおける 0 次ホールドは，インパルス列 q (t) を階段関数の信号 y (t) に変換する．一方，実装モデルにおける D/A 変換器と SH は，離散時間信号 y [n] を階段関数の信号 y (t) に変換する．

Note: SH は，サンプリング周期毎に，入力信号をごく短時間保持して出力する機能であり，論理モデルにおけるサンプラーとは全く異なる．

以上から明らかな通り，ディジタル信号処理の実装モデルにはインパルス列は存在しない．単位インパルス関数は物理的には実存しない理論上，想像上の関数であるのと同様に，インパルス列も理論上，想像上の概念である．一方，9.9 に述べた通り，システム伝達関数はシステムに入出力されるインパルス列のラプラス変換の比，即ち Z 変換の比を記述する．即ち，ディジタル信号処理の論理モデルは，実存しない想像上の信号の関係を論じているのである．従って，システム伝達関数がシステムに入出力される離散時間信号の比を記述していると誤解して，ディジタルフィルタを実装しても期待した特性のフィルタは得られないのである．

Note: 非常に不思議な事に多くのディジタル信号処理の教科書では，本資料の9.2サンプル値の表現，及び9.3 Z 変換の導出の部分が省略されている．9.4 に示した通り Z 変換は離散時間信号を元に定義されているため，これらの知識が無いと，Z 変換は離散時間信号の母関数の一種であると理解してしまい，システム伝達関数はシステムに入出力される離散時間信号の比を記述していると誤解するのである．

10.2. インパルス列と階段関数の信号の関係

システム伝達関数をディジタル信号処理の実装モデルに適用するために，同一の離散時間信号で表示される，論理モデルのインパルス列と実装モデルの階段関数の信号との関係を示す．階段関数の信号とは連続時間信号の長方形近似であるから，論理モデルのインパルス列を実装モデルの階段関数の信号の近似と考える．ここで，係数が x [n] となる，階段関数の中の一つの長方形と，インパルス列中の一つのインパルスを図10‑3 に示す．サンプリング周期は T とする．

図10-3: 長方形とインパルス．

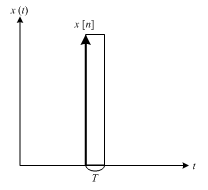
この近似の精度は長方形とインパルスの面積比から与えられる．単位インパルス関数の定義より，上記のインパルスの面積は以下となる．

$$\begin{array}{}\text{(10-1)}& x\left[n\right]{\int }_{-\infty }^{\infty }\delta \left(t-nT\right)dt=x\left[n\right]\end{array}$$

一方，上記の長方形の面積は T x [n] であるから，階段関数の信号を，これと同一の離散時間信号で表示されるインパルス列で近似すると 1 / T 倍の「近似」となる．即ち，ある離散時間信号で表示された階段関数の信号を，同じ離散時間信号で表示されたインパルス列に変換すると，1 / T 倍のゲインが生じる．同様に，ある離散時間信号で表示されたインパルス列を，同じ離散時間信号で表示された階段関数の信号に変換すると T 倍のゲインが生じる．

従って，図10‑1 に示したディジタル信号処理の実装モデルにおける離散時間信号 x [n] は階段関数の信号の係数であるから，システム伝達関数を実装モデルに適用する場合は，これを T 倍する必要がある．同様に，ディジタル信号処理の論理モデルにおける離散時間信号 y [n] はインパルス列 q (t) の係数であるから，0 次ホールドの伝達関数を実装モデルに適用する場合は，これを1 / T 倍する必要がある．

これが，9.10 に示したローパスフィルタの例において，サンプリング周波数を 1 [MHz] = 10⁶ [Hz] としたため，ゲインの最大値が 120 dB 以上となった理由である．また，ディジタル信号処理の教科書における離散時間信号やシステム伝達関数等の式の係数が微妙に異なる理由でもある．

10.3. ゲインを補正したローパスフィルタの例

9.10 に示したローパスフィルタのシステム伝達関数は，上に述べた論理モデルのインパルス列と実装モデルの階段関数の信号とのゲインの関係に基づいて，以下の通り補正される．

$$\begin{array}{}\text{(10-2)}& TH\left(z\right)=\frac{{\omega }_{c}T}{1-e^{-{\omega }_{c}T}{\mathrm{<mspace\; width="0.1em"></mspace>}z}^{-1}}\end{array}$$

また，上記のゲインが補正されたシステム伝達関数に対応する，周波数伝達関数を以下に示す．

$$\begin{array}{}\text{(10-3)}& TH\left(e^{j\omega T}\right)=\frac{{\omega }_{c}T}{1-e^{-{\omega }_{c}T}{e}^{-j\omega T}}\end{array}$$

上記の周波数伝達関数のゲイン線図を図10‑4に示す．横軸の角周波数は ω / ω_c として正規化されている．また図中の青線は正規化されたナイキスト周波数 fn を示しており，この例ではカットオフ周波数 ω_c の 20 倍の角周波数としている．

図10-4: ゲインを補正ローパスフィルタのゲイン線図の例．

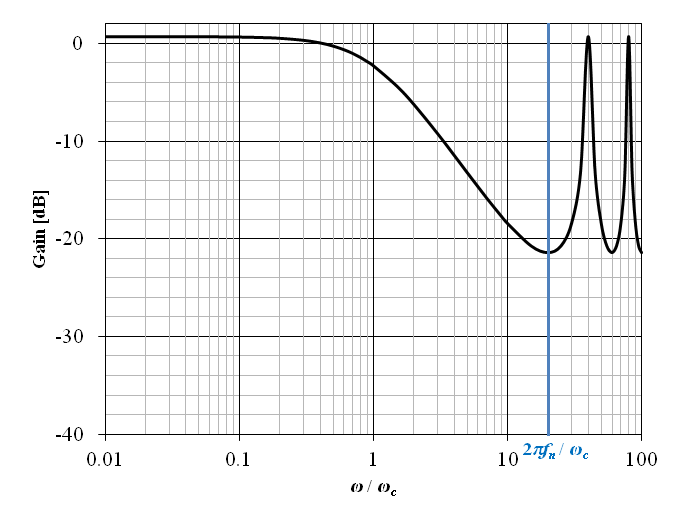
上記のゲイン線図と図6-8 に示した一次遅れ要素 (ローパスフィルタ) のゲイン線図を比較すると，ナイキスト周波数以下の特性は一見似ている様に見えるが，ゲインの最大値が 0 dB 以上 (この例では約 0.7 dB，約 1.08 倍) となっており特性が微妙に異なるローパスフィルタとなっている．

ここで，ゲインが補正された周波数伝達関数における，直流のゲインを以下に示す．

$$\begin{array}{}\text{(10-4)}& \underset{\omega \to 0}{\lim }T\mathrm{<mspace\; width="0.1em"></mspace>}H\left(e^{j\omega T}\right)=\underset{\omega \to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{{\omega }_{c}T}{1-e^{-{\omega }_{c}T}{e}^{-j\omega T}}=\frac{{\omega }_{c}T}{1-e^{-{\omega }_{c}T}}\end{array}$$

上記の式の指数関数をテーラー展開すれば，ゲインが約 1 倍となる事は判るが，明らかに厳密に 1 倍とはならない．この誤差の主な要因は，実装モデルでは階段関数の信号によって，連続時間信号を近似している点にある．(根拠は後述する)．階段関数によって近似された連続時間信号の例を図10-5 に示す．

図10-5: 階段関数による連続時間信号の近似．

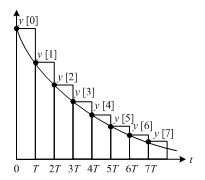
図に示した様な下に凸な関数を階段関数で近似した場合，元の関数より過大な関数となる．同様に上に凸な関数を階段関数で近似した場合，元の関数より過小な関数となる．

10.4. 階段関数の信号による誤差の補正

そこで，アナログフィルタに基づいて設計したディジタルフィルタにおいて，階段関数の信号によって連続時間信号を近似した事により生じる誤差の補正方法を示す．ここで，階段関数の信号で表示されるインパルス応答を，アナログフィルタのインパルス応答の近似と考える．この近似の精度は，アナログフィルタとディジタルフィルタにおける，時間 0 から ∞ の間のインパルス応答の面積比から与えられる．

アナログフィルタの伝達関数を G (s)，そのインパルス応答を g (t)，ディジタル化されたフィルタのシステム伝達関数を H (z)，そのインパルス応答の離散時間信号を h [n] とする．ここで，時間 0 から ∞ におけるインパルス応答 g (t) の面積は以下で与えられる．

$$\begin{array}{}\text{(10-5)}& {\int }_0^{\infty }g\left(t\right)\mathit{dt}=<mspace\; width="0.1em"></mspace>\underset{s\to 0}{\lim }G\left(s\right)\end{array}$$

上記は一見不思議な式であるが，式 (5-1) に示したラプラス変換の定義から以下の通り求められる．

$$\begin{array}{}\text{(10-6)}& \underset{s\to 0}{\lim }F\left(s\right)=\underset{s\to 0}{\lim }{\int }_0^{\infty }f\left(t\right)e^{-st}dt={\int }_0^{\infty }f\left(t\right)dt\end{array}$$

一方，10.2 に基づいてゲインが補正されたシステム伝達関数 T H (z) における，インパルス応答の離散時間信号は T h [n] となる．このゲインが補正されたインパルス応答のインパルス列の面積は，階段関数の信号によるインパルス応答の面積と等しいため，時間 0 から ∞ における階段関数の信号によるインパルス応答の面積は以下で与えられる．

$$\begin{array}{}\text{(10-7)}& \sum _{n=0}^{\infty }T\mathrm{<mspace\; width="0.1em"></mspace>}h\left[n\right]=T\mathrm{<mspace\; width="0.1em"></mspace>}\underset{z\to 1}{\lim }H\left(z\right)\end{array}$$

従って，階段関数の信号による誤差を補正したシステム伝達関数 H_N (z) は以下で与えられる．

$$\begin{array}{}\text{(10-8)}& H_N\left(z\right)=\frac{\underset{s\to 0}{\lim }G\left(s\right)}{T\underset{z\to 1}{\lim }H\left(z\right)}TH\left(z\right)=\frac{\underset{s\to 0}{\lim }G\left(s\right)}{\underset{z\to 1}{\lim }H\left(z\right)}H\left(z\right)\end{array}$$

Note: 本資料では以降，実装モデルにおいてゲインが適正となる様に補正したシステム伝達関数を，正規化システム伝達関数 H_N (z) と記す．

10.3 の伝達関数の補正において周波数伝達関数の直流の際のゲインを論じたが，これは伝達関数やボード線図を読み解く際の技法である．一方，上記の正規化システム伝達関数における s → 0, z → 1 と，直流のゲインを求める際の ω → 0 は同じ事を意味している．即ち，ディジタルフィルタのインパルス応答が，アナログフィルタのインパルス応答を近似する様にシステム伝達関数を補正する方法は，これらの直流におけるゲインが等しくなる様に補正する技法と論理的に等価となる．この方法は周波数伝達関数の直流におけるゲインが 0 倍となるか，発散し無い限り適用できる．

Note: 式 (10‑4) は，正規化された周波数伝達関数における直流のゲインを示しているが，以上の議論より，これは正規化システム伝達関数 H_N (z) のインパルス応答を表示する階段関数の信号の面積と等しい．従って，階段関数の信号による連続時間信号の近似が，この誤差の主な要因となる．

10.5. 誤差を補正したローパスフィルタの例

9.10 に述べたローパスフィルタのシステム伝達関数を，上記のアナログフィルタとディジタルフィルタのインパルス応答の関係に基づいて補正した例を示す．9.10 に述べたローパスフィルタの伝達関数を以下に再掲する．

$$\begin{array}{}\text{(10-9)}& G\left(s\right)=\frac{1}{\tau s+1}=\frac{{\omega }_c}{s+{\omega }_c}\end{array}$$

また，上記の伝達関数に対応するシステム伝達関数を以下に再掲する．

$$\begin{array}{}\text{(10-10)}& H\left(z\right)=\frac{{\omega }_c}{1-e^{-{\omega }_{c}T}{\mathrm{<mspace\; width="0.1em"></mspace>}z}^{-1}}\end{array}$$

従って，正規化システム伝達関数は以下で与えられる．

$$\begin{array}{}\text{(10-11)}& H_N\left(z\right)=\frac{\underset{s\to 0}{\lim }G\left(s\right)}{\underset{z\to 1}{\lim }H\left(z\right)}H\left(z\right)=\frac{1-e^{-{\omega }_{c}T}}{1-e^{-{\omega }_{c}T}{\mathrm{<mspace\; width="0.1em"></mspace>}z}^{-1}}\end{array}$$

上記の正規化システム伝達関数に対応する，周波数伝達関数を以下に示す．

$$\begin{array}{}\text{(10-12)}& H_N\left(e^{j\omega T}\right)=\frac{1-e^{-{\omega }_{c}T}}{1-e^{-{\omega }_{c}T}{e}^{-j\omega T}}\end{array}$$

上記の周波数伝達関数のゲイン線図を図10‑6に示す．横軸の角周波数は ω / ω_c として正規化されている．また図中の青線は正規化されたナイキスト周波数 fn を示しており，この例ではカットオフ周波数 ω_c の 20 倍の角周波数としている．

図10-6: 正規化されたローパスフィルタのゲイン線図の例．

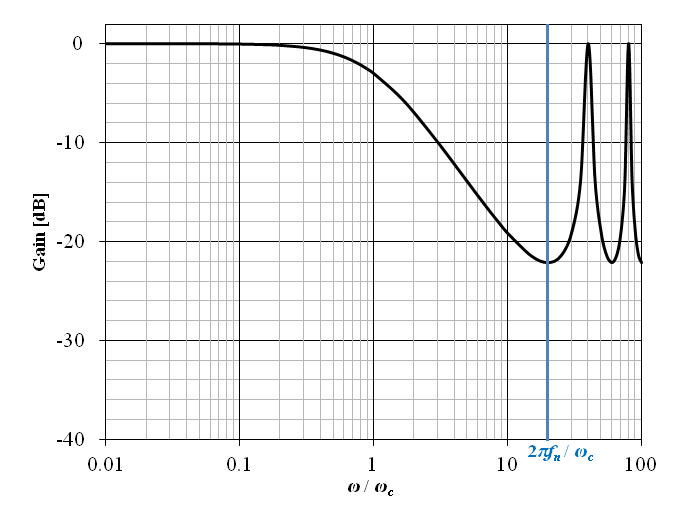
上記のゲイン線図と図6-8 に示した一次遅れ要素 (ローパスフィルタ) のゲイン線図を比較すると，ナイキスト周波数以下の特性は高い精度で一致する．

10.6. 0 次ホールドの伝達関数

ディジタル信号処理の論理モデルにおける 0 次ホールドは，インパルス列を階段関数の信号に変換する．単位インパルス関数は，単位ステップ関数の微分であるから，0 次ホールドはインパルス列中の単位インパルス関数を積分してステップ関数とし，サンプリング周期 T が経過した時点でそれを反転する事によってインパルス列を階段関数の信号に変換する．従って 0 次ホールドの伝達関数 G (s) は以下で与えられる．

$$\begin{array}{}\text{(10-13)}& G\left(s\right)=\frac{1}{s}-\frac{e^{-sT}}{s}=\frac{1-e^{-sT}}{s}\end{array}$$

10.2 に述べた通り，上記の正規化伝達関数 G_N (s) は以下で与えられる．

$$\begin{array}{}\text{(10-14)}& G_N\left(s\right)=\frac{1}{T}G\left(s\right)=\frac{1-e^{-sT}}{sT}\end{array}$$

従って，上記の周波数伝達関数は以下の通りとなる．

$$\begin{array}{}\text{(10-15)}& G_N\left(j\omega \right)=\frac{1-e^{-j\omega T}}{j\omega T}\end{array}$$

この 0 次ホールドの伝達関数は，システム伝達関数や正規化システム伝達関数には含まれていないため，ディジタルフィルタを設計する際には，正規化システム伝達関数に基づく周波数伝達関数に加えて，0 次ホールドの周波数伝達関数も考慮しなければならない事に注意せよ．

Note: 0 次ホールドの伝達関数を D/A 変換器の伝達関数と誤解しない事．D/A 変換器は離散時間信号を階段関数の信号に変換するが，これらの関係は定数係数線形常微分方程式で記述出来ないため，伝達関数も周波数伝達関数も定義されない．

上記の周波数伝達関数ボード線図を図10‑7に示す．横軸の角周波数は ωT として正規化されている．また図中の青線は正規化されたナイキスト周波数を示している．

図10-7: 0 次ホールドのボード線図．

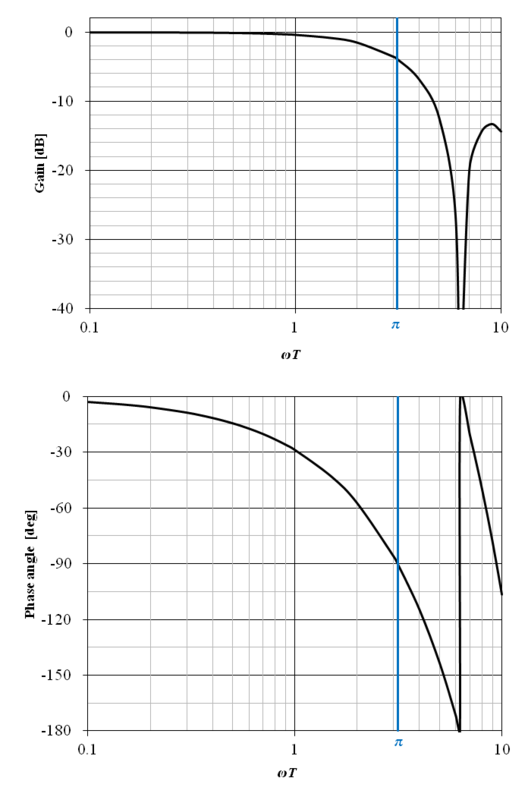
図から明らかな通り，0 次ホールドのゲインは，ナイキスト周波数において約 −3.9 [dB] (約 0.64倍)，位相は −90 [deg] となる．この様なゲインの低下，位相の遅れを避けるために，D/A 変換器のサンプリング周波数を，ディジタル信号処理のサンプリング周波数の数倍として，更に離散時間信号を補間して D/A 変換器の入力とする技法が用いられる場合がある．

本章の参考文献

筆者, "修士論文," 某大学大学院工学研究科, 1986.

Note: 筆者の修論のテーマは自動制御理論でもディジタル信号処理でも無い．無論これらを道具として最大限活用したが，研究対象とはしていない．10.3, 10.4, 10.5は，実験データを分析する過程で，データをフィルタリングすると精度が低下する事象が生じたため，一晩徹夜して問題を解決した際に見出したものである．

2017/5/29 10.4 を一部修正．