6. 伝達関数と周波数応答 - 趣味人のブログ

本章では，先ず伝達関数の定義，伝達関数の例，線形時不変システムの応答と伝達関数の関係を復習する．これらは教科書に十分な説明が記載されているため，本資料では数式の証明や導出等は省略し，留意すべき点を Note に示す．次に，6.4 において，周波数伝達関数はシステムの入出力の関係を記述する定数係数線形常微分方程式の定常解から定義される事を示し，初期条件が 0 とならず伝達関数が定義されないシステムにおいても，周波数伝達関数は定義される事を明らかにする．最後に 6.5 においてボード線図を復習する．

6.1. 伝達関数の定義
6.2. 伝達関数の例
6.3. 線形時不変システムの応答と伝達関数の関係
- インパルス応答
- インディシャル応答 (単位ステップ応答)
6.4. 周波数伝達関数の定義
6.5. ボード線図
余談: 本資料の周波数伝達関数の定義
本章の参考文献

6.1. 伝達関数の定義

入力の時間関数 x (t), (t ≥ 0) に対する出力の時間関数 y (t), (t ≥ 0) が，以下の定数係数線形常微分方程式で記述され，かつ初期条件が全て 0 となる線形時不変システムにおける，入力 x (t) と出力 y (t) のラプラス変換の比を，このシステムの伝達関数と言う．

$\begin{matrix} (6-1) & a_{n} y^{(n)} (t) + a_{(n - 1)} y^{(n - 1)} (t) + \dots + a_{1} y' (t) + a_{0} y (t) = x (t) \end{matrix}$

初期条件を以下に示す．

$\begin{matrix} (6-2) & y^{(n - 1)} (0) = y^{(n - 2)} (0) = \dots = y' (0) = y (0) = 0 \end{matrix}$

上記の初期条件における，式 (6-1) のラプラス変換を以下に示す．

$\begin{matrix} (6-3) & (a_{n} s^{n} + a_{(n - 1)} s^{(n - 1)} + \dots + a_{1} s + a_{0}) Y (s) = X (s) \end{matrix}$

ここで，X (s), Y (s) は各々原関数 x (t), y (t) の像関数を表す．これを Y (s) について解くと以下の通りとなる．

$\begin{matrix} (6-4) & Y (s) = \frac{X (s)}{a_{n} s^{n} + a_{(n - 1)} s^{(n - 1)} + \dots + a_{1} s + a_{0}} \end{matrix}$

よって，伝達関数 G (s) は以下で与えられる．

$\begin{matrix} (6-5) & G (s) = \frac{Y (s)}{X (s)} = \frac{1}{a_{n} s^{n} + a_{(n - 1)} s^{(n - 1)} + \dots + a_{1} s + a_{0}} \end{matrix}$

Note: 4.6 に述べた通り，定数係数線形常微分方程式の初期条件が全て 0 という事は，この方程式によって記述されるシステムが線形時不変システムである事を意味している．これは，式 (6-4) には零状態応答に対応する項のみが含まれ，零入力応答に対応する項が含まれないため，入力に対する重ね合わせの原理が成立する事からも明らかである．逆に言うと，定数係数線形常微分方程式の初期条件が 0 とならない場合，即ち零入力応答があるシステムには，伝達関数は定義されない．

6.2. 伝達関数の例

ローパスフィルタ (積分回路)

図6‑1 に示す，抵抗値が R [Ω] の抵抗，及びキャパシタンスが C [F] のコンデンサから成るローパスフィルタ (積分回路) の伝達関数を求める．ここで，入力電圧，出力電圧を各々 x (t), y (t) [V]，回路に流れる電流を i (t) [A] とする．

f:id:suzumushi0:20170611122124p:plain — **図6-1: ローパスフィルタ．**

式 (3‑16) より，キャパシタンスに流れる電流 i (t) [A] とこれに加わる出力電圧 y (t) [V] には以下の関係がある．

$\begin{matrix} (6-6) & i (t) = C y^{'} (t) \end{matrix}$

また，抵抗に流れる電流 i (t) [A] と入力電圧 x (t) [V] には以下の関係がある．

$\begin{matrix} (6-7) & x (t) = R i (t) + y (t) \end{matrix}$

従って，上記の回路の入力電圧，出力電圧の関係は以下の定数係数線形常微分方程式で与えられる．

$\begin{matrix} (6-8) & C R y^{'} (t) + y (t) = x (t) \end{matrix}$

上記のラプラス変換を以下に示す．

$\begin{matrix} (6-9) & C R \{s Y (s) - y (0)\} + Y (s) = X (s) \end{matrix}$

伝達関数は初期条件 y (0) = 0 を前提としているから，上記のローパスフィルタの伝達関数 G (s) は以下となる．ここで τ = CR は時定数と呼ばれる．また，角周波数 ω_c = 1 / τ はカットオフ周波数と呼ばれる．

$\begin{matrix} (6-10) & G (s) = \frac{Y (s)}{X (s)} = \frac{1}{C R s + 1} = \frac{1}{τ s + 1} = \frac{ω_{c}}{s + ω_{c}} \end{matrix}$

上記の様に，分母の次数が 1 となる伝達関数を 1 次遅れの伝達関数と言う．
Note: 上記の回路の動作は，現実には入出力に接続される回路のインピーダンスの影響を受けるため，正確な動作が要求される場合は，演算増幅器 (オペアンプ) 等を使用するのが普通である．

ハイパスフィルタ (微分回路)

図6‑2に示す，抵抗値が R [Ω] の抵抗，及びキャパシタンスが C [F] のコンデンサから成るハイパスフィルタ (微分回路) の伝達関数を求める．ここで，入力電圧，出力電圧を各々 x (t), y (t) [V]，回路に流れる電流を i (t) [A] とする．

f:id:suzumushi0:20170611122125p:plain — **図6-2: ハイパスフィルタ．**

式 (3‑16) より，キャパシタンスに流れる電流 i (t) [A] とこれに加わる入力電圧と出力電圧の差分 x (t) − y (t) [V] には以下の関係がある．

$\begin{matrix} (6-11) & \frac{1}{C} \int_{0}^{t} i (τ) d τ = x (t) - y (t) \end{matrix}$

また，抵抗に流れる電流 i (t) [A] と出力電圧 y (t) [V] には以下の関係がある．

$\begin{matrix} (6-12) & y (t) = R i (t) \end{matrix}$

従って，上記の回路の入力電圧，出力電圧の関係は以下の方程式で与えられる．

$\begin{matrix} (6-13) & y (t) + \frac{1}{C R} \int_{0}^{t} y (t) d t = x (t) \end{matrix}$

上記のラプラス変換を以下に示す．

$\begin{matrix} (6-14) & Y (s) + \frac{1}{C R s} Y (s) = X (s) \end{matrix}$

よって，上記のハイパスフィルタの伝達関数 G (s) は以下となる．ここで τ = CR は時定数と呼ばれる．また，角周波数 ω_c = 1 / τ はカットオフ周波数と呼ばれる．

$\begin{matrix} (6-15) & G (s) = \frac{Y (s)}{X (s)} = \frac{C R s}{C R s + 1} = \frac{τ s}{τ s + 1} = 1 - \frac{1}{τ s + 1} = 1 - \frac{ω_{c}}{s + ω_{c}} \end{matrix}$

Note: 上記の回路の動作も，現実には入出力に接続される回路のインピーダンスの影響を受けるが，演算増幅器 (オペアンプ) 等を使用しても，増幅器の周波数特性による制限を受け，現実にはバンドパス特性のフィルタとなるため，正確な実現は非常に困難である．

バネマスダンパ系

図6‑3 に示す，ばね定数が k [N/m] のバネ，質量が m [Kg] のマス，減衰係数 (ダンピング係数) が c [Ns/m] のダンパ (ダッシュポット) から成るバネマスダンパ系において，入力を x (t) [N] の外力，出力を y (t) [m] の変位とした際の伝達関数を求める．

f:id:suzumushi0:20170611122126p:plain — **図6-3: バネマスダンパ系．**

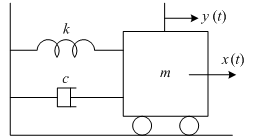
上記の運動方程式を以下に示す．

$\begin{matrix} (6-16) & m y^{''} (t) + c y^{'} (t) + k y (t) = x (t) \end{matrix}$

上記のラプラス変換を以下に示す．

$\begin{matrix} (6-17) & m \{s^{2} Y (s) - s y (0) - y^{'} (0)\} + c \{s Y (s) - y (0)\} + k Y (s) = X (s) \end{matrix}$

伝達関数は初期条件 y' (0) = y (0) = 0 を前提としているから，上記のバネマスダンパ系の伝達関数 G (s) は以下で与えられる．

$\begin{matrix} (6-18) & G (s) = \frac{Y (s)}{X (s)} = \frac{1}{m s^{2} + c s + k} \end{matrix}$

上記の様に，分母の次数が 2 となる伝達関数を 2 次遅れの伝達関数と言う．尚，振動解析ではこの式を下記の様に変形させる場合が多い．

$\begin{matrix} (6-19) & \begin{matrix} \begin{matrix} G (s) = \frac{Y (s)}{X (s)} = \frac{m^{- 1}}{s^{2} + 2 ζ ω_{0} s + {ω_{0}}^{2}} \\ ω_{0} = \sqrt{\frac{k}{m}} \\ ζ = \frac{c}{2 \sqrt{m k}} \end{matrix} \end{matrix} \end{matrix}$

ここで，ω₀ は無減衰固有角周波数，ζ は減衰比と呼ばれる．ζ > 1 の場合は G (s) の極は実数で単極，ζ < 1 の場合は複素数となるから，伝達関数をこの様に変形する事によって，応答が指数的なのか振動的なのか，また固有振動数が容易に判る．

Note: 振動解析では，上記の様に外力によって引き起こされる振動を強制振動 (強制応答) と言う．

直列共振回路

図6‑4 に示す，抵抗値が R [Ω] の抵抗，インダクタンスが L [H] のコイル，及びキャパシタンスが C [F] のコンデンサから成る直列共振回路の伝達関数を求める．ここで，入力電圧，出力電圧を各々 x (t), y (t) [V]，回路に流れる電流を i (t) [A] とする．

f:id:suzumushi0:20170611122127p:plain — **図6-4: 直列共振回路．**

式 (3‑16) より，キャパシタンスに流れる電流 i (t) [A] とこれに加わる出力電圧 y (t) [V] には以下の関係がある．

$\begin{matrix} (6-20) & i (t) = C y^{'} (t) \end{matrix}$

また，式 (3‑9) より，抵抗，コイルに流れる電流 i (t) [A] と入力電圧 x (t) [V] には以下の関係がある．

$\begin{matrix} (6-21) & x (t) = R i (t) + L i^{'} (t) + y (t) \end{matrix}$

従って，上記の回路の入力電圧，出力電圧の関係は以下の定数係数線形常微分方程式で与えられる．

$\begin{matrix} (6-22) & C L y^{''} (t) + C R y^{'} (t) + y (t) = x (t) \end{matrix}$

上記のラプラス変換を以下に示す．

$\begin{matrix} (6-23) & C L \{s^{2} Y (s) - s y (0) - y^{'} (0)\} + C R \{s Y (s) - y (0)\} + Y (s) = X (s) \end{matrix}$

伝達関数は初期条件 y' (0) = y (0) = 0 を前提としているから，上記の直列共振回路の伝達関数 G (s) は以下で与えられる．

$\begin{matrix} (6-24) & G (s) = \frac{Y (s)}{X (s)} = \frac{1}{C L s^{2} + C R s + 1} \end{matrix}$

この伝達関数は，前記のバネマスダンパ系の伝達関数と本質的に同一となる．

むだ時間要素

システムの処理遅延等のむだ時間の伝達関数を求める．入力の時間関数を x (t)，出力の時間関数を y (t)，むだ時間を T とすると，これらの関係は以下の通りとなる．

$\begin{matrix} (6-25) & y (t) = x (t - T) \end{matrix}$

表5-2 に示した時間軸上の平行移動の定理より，上記のラプラス変換は以下で与えられる．

$\begin{matrix} (6-26) & Y (s) = e^{- T s} X (s) \end{matrix}$

従って，むだ時間要素の伝達関数 G (s) は以下で与えられる．

$\begin{matrix} (6-27) & G (s) = \frac{Y (s)}{X (s)} = e^{- T s} \end{matrix}$

むだ時間要素の伝達関数は，システムに処理遅延がある場合だけでなく，サンプリングによるディジタル信号処理においても使用される．

フィードバック系

以下のブロックダイヤグラムで表される，伝達関数 G (s), H (s) から成るフィードバック系の伝達関数を求める．

f:id:suzumushi0:20170611122128p:plain — **図6-5: フィードバック系のブロックダイヤグラム．**

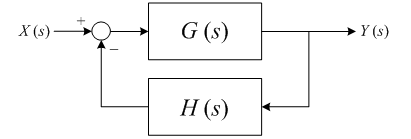
入力の時間関数を x (t)，出力の時間関数を y (t) とすると，これらの像関数 X (s), Y (s) の関係は以下で与えられる．

$\begin{matrix} (6-28) & \begin{matrix} \begin{matrix} Y (s) = \{X (s) - H (s) Y (s)\} G (s) \\ ∴ \{1 + G (s) H (s)\} Y (s) = G (s) X (s) \end{matrix} \end{matrix} \end{matrix}$

従って，上記のブロックダイヤグラムで示されるフィードバック系の伝達関数 Y (s) / X (s) は以下で与えられる．

$\begin{matrix} (6-29) & \frac{Y (s)}{X (s)} = \frac{G (s)}{1 + G (s) H (s)} \end{matrix}$

6.3. 線形時不変システムの応答と伝達関数の関係

インパルス応答

伝達関数 G (s) は入力の時間関数 x (t) と出力の時間関数 y (t) のラプラス変換の比であるから，これらの像関数 X (s), Y (s) の関係は以下の通りとなる．

$\begin{matrix} (6-30) & Y (s) = X (s) G (s) \end{matrix}$

ここで，入力を単位インパルス関数 δ (t) とした際の出力の時間関数をインパルス応答と言う．5.2 に述べた通り，単位インパルス関数のラプラス変換は 1 であるから，1 G (s) はインパルス応答のラプラス変換を示している．式 (6‑30) は以下の通り書き直せる．

$\begin{matrix} (6-31) & Y (s) = X (s) 1 G (s) \end{matrix}$

上記の式と 5.2 に示した畳み込の公式より，システムのインパルス応答 g (t) が与えられれば，任意の入力の時間関数 x (t) に対する出力の時間関数 y (t) は以下の畳み込積分から得られる．

$\begin{matrix} (6-32) & y (t) = \int_{0}^{t} g (τ) x (t - τ) d τ \end{matrix}$

インディシャル応答 (単位ステップ応答)

残念ながら，単位インパルス関数は理論上，想像上の関数であるため，インパルス応答は物理的には実存しない．しかし，入力を単位ステップ関数 u (t) とした際の出力の時間関数であるインディシャル応答 (単位ステップ応答) からも類似の関係が得られる．単位ステップ関数のラプラス変換は 1 / s であるから，インディシャル応答のラプラス変換を A (s) とすると，これらの関係は以下の式で与えられる．

$\begin{matrix} (6-33) & A (s) = \frac{1}{s} G (s) \end{matrix}$

よって，式 (6-30) は以下の通り書き直せる．

$\begin{matrix} (6-34) & Y (s) = s A (s) X (s) \end{matrix}$

上記の式と 5.2 に示した畳み込の公式，及び微分の公式より，システムのインディシャル応答 a (t) が与えられれば，任意の入力の時間関数 x (t) に対する出力の時間関数 y (t) は以下の式から得られる．

$\begin{matrix} (6-35) & y (t) = \frac{d}{d t} \{\int_{0}^{t} a (τ) x (t - τ) d τ\} = \int_{0}^{t} a (τ) \frac{d}{d t} x (t - τ) d τ + a (t) f (0) \end{matrix}$

Note: 以上の関係は，あくまで伝達関数が定義される線形時不変システムにおいて成立する事に注意せよ．即ち，これらの関係は，初期条件が 0 とならならず伝達関数が定義されないシステムにおいては成立しない．

6.4. 周波数伝達関数の定義

入力の時間関数 x (t) に対する出力の時間関数 y (t) が，以下の定数係数線形常微分方程式で記述されるシステムに対して，入力 x (t) を複素正弦波 e ^jωtとし，出力 y (t) が入力と角周波数が等しい複素正弦波となる定常状態における入力 x (t) と出力 y (t) の比を，このシステムの周波数伝達関数 (周波数応答) と言う．

$\begin{matrix} (6-36) & a_{n} y^{(n)} (t) + a_{(n - 1)} y^{(n - 1)} (t) + \dots + a_{1} y' (t) + a_{0} y (t) = x (t) \end{matrix}$

4.4 及び 4.5 に述べた通り，定常状態における出力 y (t) は，上記の定数係数線形常微分方程式における非同次方程式の特殊解 (定常解) y_p(t) となる．よって，上記の式に，x (t) = e ^jωt を，また 4.4に述べた未定係数法に基づいて y (t) = A e ^j^{(ωt + φ)} を代入すると，以下の通りとなる．

$\begin{matrix} (6-37) & \{a_{n} {(j ω)}^{n} + a_{(n - 1)} {(j ω)}^{(n - 1)} + \dots + a_{1} (j ω) + a_{0}\} A e^{j (ω t + φ)} = e^{j ω t} \end{matrix}$

これを，入力 x (t) と出力 y (t) の比に整理すると下記の式が得られる．

$\begin{matrix} (6-38) & \frac{y (t)}{x (t)} = \frac{A e^{j (ω t + φ)}}{e^{j ω t}} = \frac{1}{a_{n} {(j ω)}^{n} + a_{(n - 1)} {(j ω)}^{(n - 1)} + \dots + a_{1} (j ω) + a_{0}} \end{matrix}$

上記の正弦波の時間関数の比における e ^jωtは約分され，時間関数が角周波数の関数に変換される．従って，周波数伝達関数 G (jω) は以下で与えられる．

$\begin{matrix} (6-39) & G (j ω) = A e^{j φ} = \frac{1}{a_{n} {(j ω)}^{n} + a_{(n - 1)} {(j ω)}^{(n - 1)} + \dots + a_{1} (j ω) + a_{0}} \end{matrix}$

ここで，以下に示す通り，周波数伝達関数 G (jω) の絶対値は，入出力される正弦波の振幅の比を，偏角は入出力される正弦波の位相差を示す．

$\begin{matrix} (6-40) & \begin{matrix} \begin{matrix} |G (j ω)| = A \\ A r g \{G (j ω)\} = φ \end{matrix} \end{matrix} \end{matrix}$

Note: 以上の説明から明らかな通り，周波数伝達関数はシステムに入出力される正弦波の定常状態における振幅の比と位相差を示したものであり，定数係数線形常微分方程式の初期条件に依存しないため，初期条件が 0 とならず伝達関数が定義されないシステムにおいても，周波数伝達関数は定義できる事に注意せよ．更に，伝達関数と異なり入出力の時間関数の定義域に (t ≥ 0) の制約が無い事にも注意せよ．

6.1 に述べた上記と同じ定数係数線形常微分方程式で記述されるシステムにおいて，式 (6‑5) に示した伝達関数の s を jω に置き換えると，式 (6‑39) に示した周波数伝達関数となる．但し，この逆は必ずしも成り立たつとは限らない．初期条件が 0 とならない場合でも，周波数伝達関数は定義できるが，伝達関数は定義されない．

Note: 周波数伝達関数は定常状態においてシステムに入出力される正弦波の振幅の比と位相差を示したものである．一方，3 章に示した複素正弦波交流における誘導リアクタンス，容量リアクタンス，レジスタンス，及びこれらの直列回路，並列回路における複素合成インピーダンスは，何れも RCL による回路をシステムとすれば，複素正弦波交流の電流を入力，電圧を出力とした際の，定常状態における電圧と電流の振幅の比と位相差を示したものと解釈する事ができる．RCL による如何なる回路も，直列回路や並列回路の組み合わせであるから，RCL 回路における周波数伝達関数を求める際には，複素正弦波交流における誘導リアクタンス，容量リアクタンス，及びレジスタンスから計算する事ができ，伝達関数から求める必要は無い．

6.5. ボード線図

周波数伝達関数 G (jω) の絶対値及び偏角と周波数の関係を図示したものをボード線図と言う．前者はゲイン線図，後者は位相線図とも呼ばれる．周波数伝達関数の絶対値は入出力される正弦波の振幅の比を，偏角は入出力される正弦波の位相差を示すため，ボード線図はこれらと周波数の関係，即ちゲイン特性や位相特性等の周波数特性を図示したものとなる．

一般に，ボード線図は横軸に周波数 [Hz]，若しくは角周波数 [rad/s] を対数目盛で取り，縦軸にG (jω) の絶対値 (Gain) をデシベル [dB] で，偏角 (Phase angle) を度 [deg] で表示する．デシベルとは，ある数値の常用対数を 20 倍したもので，20 dB の差は 10 倍を，6 dB の差は約 2 倍を意味する．|G (jω)| をデシベルで表すと以下の通りとなる．

$\begin{matrix} (6-41) & 20 {l o g}_{10} |G (j ω)| \end{matrix}$

積分要素のボード線図

以下の伝達関数で表される積分要素のボード線図を示す．

$\begin{matrix} (6-42) & G (s) = \frac{1}{s} \end{matrix}$

上記の伝達関数に対応する周波数伝達関数を以下に示す．

$\begin{matrix} (6-43) & G (j ω) = \frac{1}{j ω} \end{matrix}$

上記の周波数伝達関数のボード線図を図6‑6に示す．図から明らかな通り，ゲイン特性は −20 [dB/decade] (周波数が 10 倍となると，ゲインは −20 [dB]，即ち 1/10 倍) となる．また，位相特性は −90 [deg] (90度の位相遅れ) となる．上記から明らかな通り，積分要素のゲインは角周波数が 0 に近づくと無限大に発散するため，正確な積分要素を実現する事は出来ず，多くの場合，以下に述べるローパスフィルタ (積分回路) で代用する．

f:id:suzumushi0:20170611122129p:plain — **図6-6: 積分要素のボード線図．**

微分要素のボード線図

以下の伝達関数で表される微分要素のボード線図を示す．

$\begin{matrix} (6-44) & G (s) = s \end{matrix}$

上記の伝達関数に対応する周波数伝達関数を以下に示す．

$\begin{matrix} (6-45) & G (j ω) = j ω \end{matrix}$

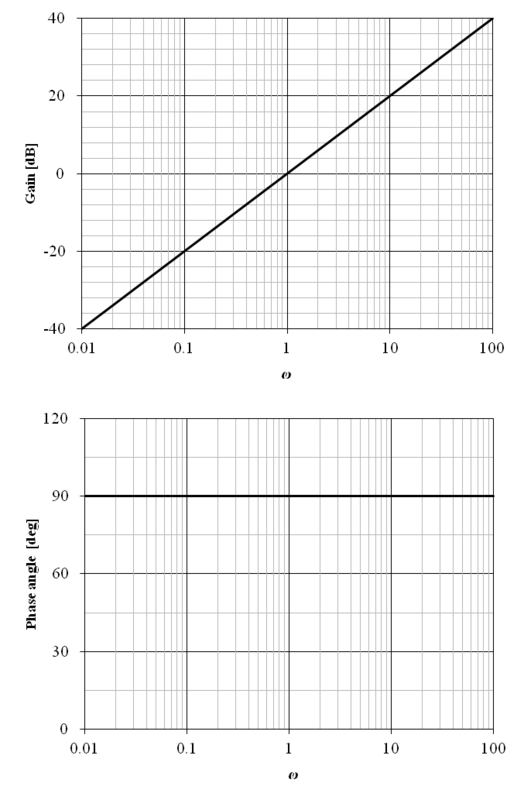
上記の周波数伝達関数のボード線図を図6‑7に示す．図から明らかな通り，ゲイン特性は 20 [dB/decade]，位相特性は 90 [deg] (90度の位相進み) となる．上記から明らかな通り，微分要素は角周波数が高い領域でゲインが高くなるため，ノイズの影響を非常に受けやすい問題点がある．また，角周波数が無限大に近づくとゲインが無限大に発散するため，正確な微分要素を実現する事は出来ない．以下に述べるハイパスフィルタ (微分回路) で代用する場合もあるが，6.2 に述べた通りこれの正確な実現も困難である．

Note: そもそも，理論的には過去から現在までの信号の変化から，その現時点での微分を求める事は出来ないため，厳密な微分要素は理論上存在しない．次の瞬間に微分可能ではない変化をするかも知れない．5.4 において，制御理論では，ラプラス変換の分子の次数が分母の次数より高い場合は扱わないと述べたが，分子の次数の方が高い場合とは微分要素があるのと等価であり，その様な物は存在し得ないため扱う必要が無いのである．

f:id:suzumushi0:20170611122130p:plain — **図6-7: 微分要素のボード線図．**

1 次遅れ要素のボード線図 (ローパスフィルタ)

以下の伝達関数で表される 1 次遅れ要素 (ローパスフィルタ，積分回路) のボード線図を示す．ここで，τ は時定数，ω_c = 1 / τ はカットオフ周波数とする．

$\begin{matrix} (6-46) & G (s) = \frac{1}{τ s + 1} = \frac{ω_{c}}{s + ω_{c}} \end{matrix}$

上記の伝達関数に対応する周波数伝達関数を以下に示す．

$\begin{matrix} (6-47) & G (j ω) = \frac{1}{1 + j ω τ} = \frac{1}{1 + j \frac{ω}{ω_{c}}} \end{matrix}$

従って，G (jω) の絶対値と偏角は以下の通りとなる．

$\begin{matrix} (6-48) & \begin{matrix} \begin{matrix} |G (j ω)| = \frac{1}{\sqrt{1 + {(ω τ)}^{2}}} = \frac{1}{\sqrt{1 + {(\frac{ω}{ω_{c}})}^{2}}} \\ A r g \{G (j ω)\} = {t a n}^{- 1} (- ω τ) = {t a n}^{- 1} (- \frac{ω}{ω_{c}}) \end{matrix} \end{matrix} \end{matrix}$

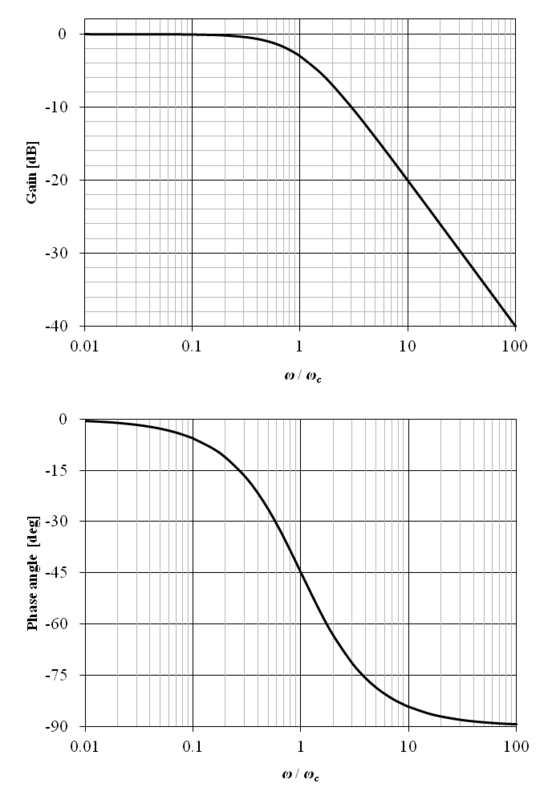
上記の周波数伝達関数のボード線図を図6‑8に示す．横軸の角周波数は ω / ω_c として正規化されている．

図から明らかな通り，ω / ω_c≪ 1 の場合のゲイン特性は 0 [dB] (1倍) となり，ω / ω_c ≫ 1 の場合は −20 [dB/decade] となる．これは，20 [dB/decade] の減衰傾斜とも呼ばれる．ここで，図の中央のカットオフ周波数 ω = ω_c におけるゲインは約 −3 [dB]，即ち約 7/10 倍となる．これは，約 3 [dB] の減衰量とも呼ばれる．また，位相は −45 [deg] となる．

従って，この伝達関数で示される1 次遅れ要素はローパスフィルタとして動作する．また，ω / ω_c ≫ 1 の周波数領域は積分要素の代用とする事ができる．

f:id:suzumushi0:20170611122131p:plain — **図6-8: 1次遅れ要素 (ローパスフィルタ) のボード線図．**

1 次遅れ要素のボード線図 (ハイパスフィルタ)

以下の伝達関数で表される 1 次遅れ要素 (ハイパスフィルタ，微分回路) のボード線図を示す．ここで，τ は時定数，ω_c = 1 / τ はカットオフ周波数とする．

$\begin{matrix} (6-49) & G (s) = \frac{τ s}{τ s + 1} = 1 - \frac{1}{τ s + 1} = 1 - \frac{ω_{c}}{s + ω_{c}} \end{matrix}$

上記の伝達関数に対応する周波数伝達関数を以下に示す．

$\begin{matrix} (6-50) & G (j ω) = \frac{j ω τ}{1 + j ω τ} = 1 - \frac{1}{1 + j ω τ} = 1 - \frac{1}{1 + j \frac{ω}{ω_{c}}} \end{matrix}$

上記の周波数伝達関数のボード線図を図6‑9に示す．横軸の角周波数は ω / ω_c として正規化されている．

図から明らかな通り，ハイパスフィルタとローパスフィルタのゲイン線図は，角周波数を逆数とした関係となる．ω / ω_c≪ 1 の場合のゲイン特性は 20 [dB/decade] となり，ω / ω_c ≫ 1 の場合は 0 [dB] となる．ここで，図の中央のカットオフ周波数 ω = ω_c におけるゲインは約 −3 [dB]，位相は 45 [deg] となる．

従って，この伝達関数で示される1 次遅れ要素はハイパスフィルタとして動作する．また，ω / ω_c≪ 1 の周波数領域は微分要素の代用とする場合がある．但し，6.2 に述べた通り，現実にはハイパスフィルタの正確な実現は困難である．

f:id:suzumushi0:20170611122132p:plain — **図6-9: 1次遅れ要素 (ハイパスフィルタ) のボード線図．**

2 次遅れ要素のボード線図

以下の伝達関数で表される 2 次遅れ要素のボード線図を示す．ここで，ω₀ は無減衰固有角周波数，ζ は減衰比とする．

$\begin{matrix} (6-51) & G (s) = \frac{{ω_{0}}^{2}}{s^{2} + 2 ζ ω_{0} s + {ω_{0}}^{2}} \end{matrix}$

上記の伝達関数に対応する周波数伝達関数を以下に示す．

$\begin{matrix} (6-52) & G (j ω) = \frac{{ω_{0}}^{2}}{{{ω_{0}}^{2} - ω}^{2} + 2 ζ ω_{0} j ω} = \frac{1}{\{1 - {(\frac{ω}{ω_{0}})}^{2}\} + j 2 ζ \frac{ω}{ω_{0}}} \end{matrix}$

Note: 上記程度の複素関数の絶対値や偏角は，Excel や関数電卓で直接計算できるため，これらの式の展開は省略する．

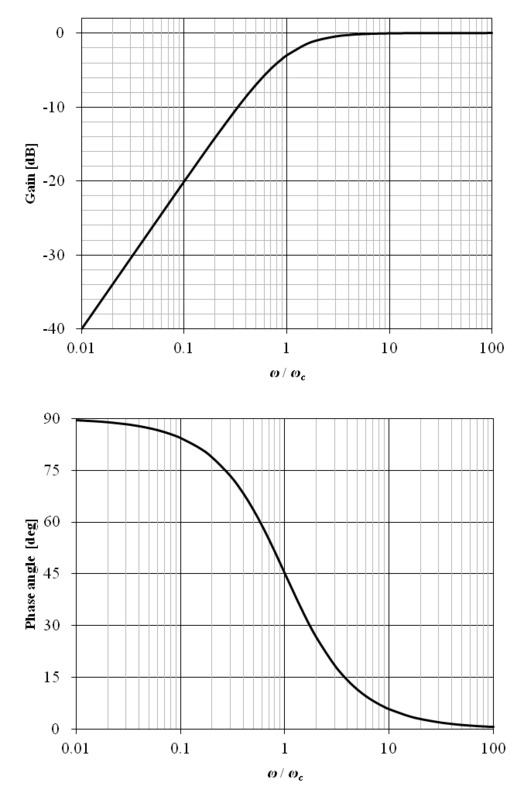
上記の周波数伝達関数のボード線図を図6‑10に示す．横軸の角周波数は ω / ω₀ として正規化されている．図から明らかな通り，ω / ω₀ ≪ 1 の場合のゲイン特性は 0 [dB] となり，ω / ω₀≫ 1 の場合は −40 [dB/decade] (周波数が 10 倍となると，ゲインは −40 [dB]，即ち 1/100 倍) となる．これは 40 [dB/decade] の減衰傾斜とも呼ばれる．ここで，図の中央の無減衰固有角周波数 ω = ω₀ 近傍におけるゲインは減衰比 ζ に依存する．また，その際の位相は −90 [deg] となる．

f:id:suzumushi0:20170611122133p:plain — **図6-10: 2次遅れ要素のボード線図．**

むだ時間要素のボード線図

以下の伝達関数で表されるむだ時間要素のボード線図を示す．

$\begin{matrix} (6-53) & G (s) = e^{- T s} \end{matrix}$

上記の伝達関数に対応する周波数伝達関数を以下に示す．

$\begin{matrix} (6-54) & G (j ω) = e^{- j ω T} \end{matrix}$

上記の周波数伝達関数のボード線図を図6‑11に示す．横軸の角周波数は ωT として正規化されている．図から明らかな通り，むだ時間要素のゲイン特性は 0 [dB] となる．また，ω = π / T となる角周波数における位相は −180 [deg] となる．従って，むだ時間要素を含むフィードバック系のシステムにおいて，角周波数 ω = π / T におけるゲインが 0 [dB] を超える場合は，発振が生じる可能性がある．

f:id:suzumushi0:20170611122134p:plain — **図6-11: むだ時間要素のボード線図．**

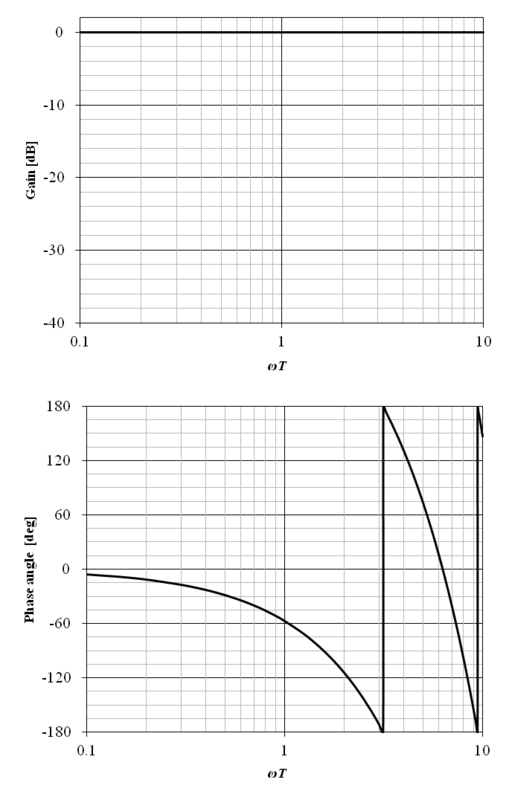
以上が，むだ時間要素の教科書的説明である．ここで，システムの処理遅延等のむだ時間が伝達関数で記述できる事を直感的に説明する．上記のむだ時間要素の位相線図の横軸を直線軸とした図を以下に示す．

f:id:suzumushi0:20170611122135p:plain — **図6-12: むだ時間要素の位相線図．**

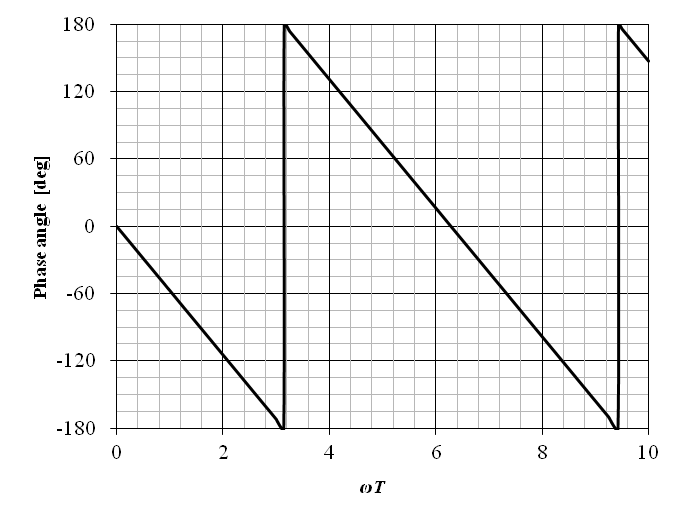
式 (6‑25) から明らかな通り，むだ時間要素とは，入力 x (t) から出力 y (t) への遅延時間が角周波数によらず一定となる要素の事である．従って，この遅延時間を周波数伝達関数における位相の遅れと考えると，むだ時間要素とは位相遅れが角周波数に比例する要素となる．むだ時間要素の周波数伝達関数は，この様な角周波数と位相遅れの関係を記述しているのである．但し，複素数の偏角の定義上，上の図に示す様に位相遅れが 180 [deg] を超えると 180 [deg] の位相進みとして表示される事に注意せよ．

Note: この考え方は，13.4 に述べる線形位相 FIR フィルタの基本となる．

余談: 本資料の周波数伝達関数の定義

6.4に述べた周波数伝達関数に関する解説は，殆どの制御工学の教科書の記述と大幅に異なるため，その理由を以下に説明する．

殆どの制御工学の教科書では，伝達関数において s = jω と変換した関数を周波数伝達関数として定義しているが，その理由が何も書かれておらず，即ち単に公式を天下り式に示しているだけで，何故そうなるのかが全く理解できない問題がある．但し，ごく一部の教科書には，伝達関数で記述された線形時不変システムの入力を正弦波とした際の，定常状態における入力と出力の比から周波数伝達関数を求める方法が示されているが，以下の観点からは説明が不足しているのである．

電気回路の周波数伝達関数を求める際に，制御工学の教科書通りに，入出力の関係を定数係数線形常微分方程式で記述し，ラプラス変換を行い，伝達関数を求めて，s = jω と変換するやり方は，正直の上に馬鹿が付く解法である．本資料の 3 章が理解できていれば，電気回路における周波数伝達関数は，回路の複素合成インピーダンスから直ちに求める事ができる．

周波数伝達関数の導出に，定数係数線形常微分方程式の記述，ラプラス変換と伝達関数の算出，伝達関数への正弦波の入力と定常状態における出力の算出といった教科書通りの手順が必要であるとすれば，何故，本資料の 3 章に示した複素合成インピーダンスに基づく遥かに簡単な解法によって，これと等価な結果が導けるのか，説明が必要なのである．即ち，制御工学の教科書の周波数伝達関数の説明では，電気工学における複素インピーダンスによる解法との関係が全く不明なのである．或いは，これらは厳密には制約条件や適用範囲が異なる問題に対する異なる解法なのか，という疑問が生じる．

本資料では電気工学と整合性の取れた周波数伝達関数の解法を示している．4.5 章に述べた通り，3 章に示した複素合成インピーダンスは，定数係数線形常微分方程式によって記述されたシステムにおいて，入力を複素正弦波 e ^jωtとし，出力を非同次方程式の特殊解 (定常解) y_p(t) から求める方法で導出している．このため，本資料でもこの方法によって，周波数伝達関数を求めている．ごく一部の制御工学の教科書に示された伝達関数から周波数伝達関数を求める解法には過渡現象が含まれてしまうため，本資料の様に定常解を直接求めた方が容易に理解できるし，初期条件に依存しないため，伝達関数が定義されない場合にも対応できる．

本章の参考文献

明石一, "制御工学増訂版," 大学講座機械工学 12, 共立出版, 1979.