7. 過渡現象

本章では，初期条件が 0 であり，伝達関数が定義される 1 次遅れ要素のインディシャル応答，ランプ応答，正弦波応答，2 次遅れ要素のインディシャル応答，正弦波応答を示す．次に，初期条件が 0 とならず伝達関数が定義されない 1 次遅れ要素，2 次遅れ要素の零入力応答を示す．最後に，同様に初期条件が 0 とならず伝達関数が定義されない 1 次遅れ要素のインディシャル応答を示し，初期条件，入力が共にある場合の出力は，これらの零入力応答と零状態応答の重ね合わせとなる事を述べる．

7.1. 1 次遅れ要素のインディシャル応答 (単位ステップ応答)

以下の伝達関数で表される 1 次遅れ要素のインディシャル応答を示す．ここで，τ は時定数とする．

$$\begin{array}{}\text{(7-1)}& G\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{1}{\tau s+1}\end{array}$$

入力及び出力の原関数を各々 x (t), y (t)，これらの像関数を各々 X (s), Y (s) とすると，入力は単位ステップ関数 x (t) = u (t), X (s) = 1 / s であるから，出力 y (t) のラプラス変換 Y (s) は以下で与えられる．

$$\begin{array}{}\text{(7-2)}& Y\left(s\right)=\frac{1}{s}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{\tau s+1}\end{array}$$

ここで，Y (s) を以下の部分分数に展開する．

$$\begin{array}{}\text{(7-3)}& Y\left(s\right)=\frac{k_1}{s}+\frac{k_2}{\tau s+1}\end{array}$$

留数定理より k₁, k₂ は以下で与えられる．

$$\begin{array}{}\text{(7-4)}& \begin{array}{}\begin{array}{c}{k}_1=\underset{s\to 0}{\lim }<mspace\; width="0.1em"></mspace>sY\left(s\right)=1\\ k_2=\underset{s\to -1/\tau }{\lim }\left(\tau s+1\right)Y\left(s\right)=-\tau \end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-5)}& Y\left(s\right)=\frac{1}{s}-\frac{\tau }{\tau s+1}=\frac{1}{s}-\frac{1}{s+{\tau }^{-1}}\end{array}$$

表5‑1 によるラプラス逆変換から，出力 y (t) は以下で与えられる．

$$\begin{array}{}\text{(7-6)}& y\left(t\right)=1-e^{-\frac{t}{\tau }},\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(t\ge 0\right)\end{array}$$

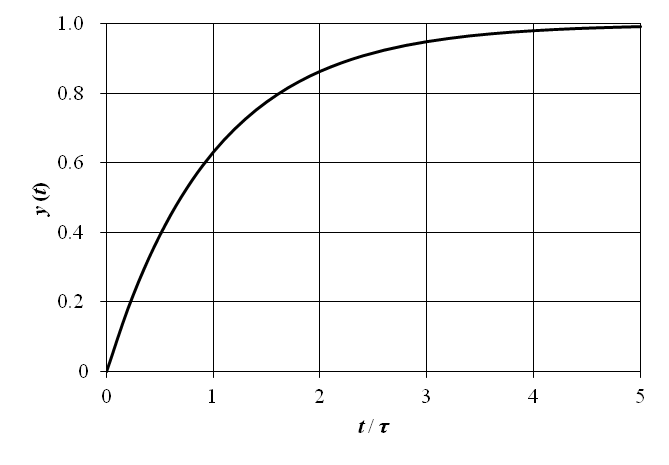
上記の 1 次遅れ要素のインディシャル応答を図7‑1 に示す．横軸の時間は t / τ として正規化されている．図から明らかな通り，出力 y (t) の立ち上がりに要する時間は，時定数 τ に反比例する．即ち時定数が小さいほど立ち上がり時間は早くなる．また，時間 t = τ において y (t) = 1 − e ⁻¹ ≃ 0.63 であるから，時定数とは，出力 y (t) が定常状態の約 0.63 倍となる時間となる．

図7-1: 1 次遅れ要素のインディシャル応答．

7.2. 1 次遅れ要素のランプ応答

以下の伝達関数で表される 1 次遅れ要素のランプ応答を示す．ここで，τ は時定数とする．

$$\begin{array}{}\text{(7-7)}& G\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{1}{\tau s+1}\end{array}$$

入力及び出力の原関数を各々 x (t), y (t)，これらの像関数を各々 X (s), Y (s) とすると，入力はランプ関数 x (t) = t, (t ≥ 0), X (s) = 1 / s² であるから，出力 y (t) のラプラス変換 Y (s) は以下で与えられる．

$$\begin{array}{}\text{(7-8)}& Y\left(s\right)=\frac{1}{s^2}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{\tau s+1}\end{array}$$

1 / s² の極は重極であるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-9)}& Y\left(s\right)=\frac{k_1}{s^2}+\frac{k_2}{s}+\frac{k_3}{\tau s+1}\end{array}$$

留数定理より k₁, k₂, k₃ は以下で与えられる．

$$\begin{array}{}\text{(7-10)}& \begin{array}{}\begin{array}{c}{k}_1=\underset{s\to 0}{\lim }<mspace\; width="0.1em"></mspace>s^{2}Y\left(s\right)=1\\ k_2=\underset{s\to 0}{\lim }\frac{d}{ds}{s}^{2}Y\left(s\right)=\underset{s\to 0}{\lim }\frac{-\tau }{{\left(\tau s+1\right)}^2}=-\tau \\ k_3=\underset{s\to -1/\tau }{\lim }\left(\tau s+1\right)Y\left(s\right)={\tau }^2\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-11)}& Y\left(s\right)=\frac{1}{s^2}-\frac{\tau }{s}+\frac{{\tau }^2}{\tau s+1}=\frac{1}{s^2}-\frac{\tau }{s}+\frac{\tau }{s+{\tau }^{-1}}\end{array}$$

表5‑1 によるラプラス逆変換から，出力 y (t) は以下で与えられる．

$$\begin{array}{}\text{(7-12)}& y\left(t\right)=t-\tau +\tau e^{-\frac{t}{\tau }}=t-\tau \left(1-e^{-\frac{t}{\tau }}\right),\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(t\ge 0\right)\end{array}$$

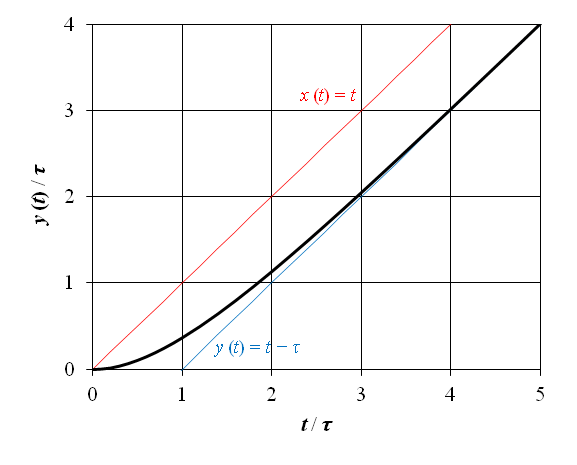
上記の 1 次遅れ要素のランプ応答を図7‑2に示す．横軸の時間は t / τ，縦軸の出力は y (t) / τ として正規化されている．図の赤線は入力のランプ関数を示している．図から明らかな通り，出力 y (t) は t → ∞ で y (t) = t − τ に漸近する．よって，定常状態における入力 x (t) と出力 y (t) の間には，y (t) = x (t) − τ の差が生じるため x (t) = y (t + τ) の関係が成立する．

図7-2: 1 次遅れ要素のランプ応答．

7.3. 1 次遅れ要素の正弦波応答

以下の伝達関数で表される 1 次遅れ要素の正弦波応答を示す．ここで，τ は時定数とする．

$$\begin{array}{}\text{(7-13)}& G\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{1}{\tau s+1}\end{array}$$

入力及び出力の原関数を各々 x (t), y (t)，これらの像関数を各々 X (s), Y (s) とし，入力を振幅 1 初期位相 0 の正弦波 x (t) = sin (ωt), (t ≥ 0), X (s) = ω / (s² + ω²) とすると，出力 y (t) のラプラス変換 Y (s) は以下で与えられる．

$$\begin{array}{}\text{(7-14)}& Y\left(s\right)=\frac{\omega }{s^2+{\omega }^2}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{\tau s+1}\end{array}$$

1 / (s² + ω²) の極は複素数であるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-15)}& Y\left(s\right)=\frac{k_{1}s+k_2}{s^2+{\omega }^2}+\frac{k_3}{\tau s+1}\end{array}$$

留数定理より k₁, k₂, k₃ は以下で与えられる．

$$\begin{array}{}\text{(7-16)}& \begin{array}{c}\begin{array}{r}\underset{s\to j\omega }{\mathrm{l}\mathrm{i}\mathrm{m}}\left(k_{1}s+k_2\right)\\ \\ \end{array}\begin{array}{l}=k_2+j\omega k_1\\ =\underset{s\to \mathit{j\omega }}{\lim }\left(s^2+{\omega }^2\right)Y\left(s\right)\\ =\underset{s\to j\omega }{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\omega }{\tau s+1}=\frac{\omega -j{\omega }^2\tau }{1+{\left(\omega \tau \right)}^2}\end{array}\\ \therefore k_1=\frac{-\omega \tau }{1+{\left(\omega \tau \right)}^2},\mathrm{<mspace\; width="0.4em"></mspace>}\mathrm{<mspace\; width="0.4em"></mspace>}{k}_2=\frac{\omega }{1+{\left(\omega \tau \right)}^2}\\ k_3=\underset{s\to -1/\tau }{\lim }<mspace\; width="0.1em"></mspace>\left(\tau s+1\right)Y\left(s\right)=\frac{\omega {\tau }^2}{1+{\left(\omega \tau \right)}^2}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-17)}& Y\left(s\right)=\frac{\omega \tau }{1+{\left(\omega \tau \right)}^2}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{s+{\tau }^{-1}}+\frac{1}{1+{\left(\omega \tau \right)}^2}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{\omega }{s^2+{\omega }^2}-\frac{\omega \tau }{1+{\left(\omega \tau \right)}^2}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{s}{s^2+{\omega }^2}\end{array}$$

表5‑1 によるラプラス逆変換，及び式 (1‑14) に示した三角関数の合成定理から，出力 y (t) は以下で与えられる．

$$\begin{array}{}\text{(7-18)}& \begin{array}{}\begin{array}{r}y\left(t\right)\\ \end{array}\begin{array}{l}=\frac{\omega \tau }{1+{\left(\omega \tau \right)}^2}{e}^{-\frac{t}{\tau }}+\frac{1}{1+{\left(\omega \tau \right)}^2}\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)-\frac{\omega \tau }{1+{\left(\omega \tau \right)}^2}\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)\\ =\frac{\omega \tau }{1+{\left(\omega \tau \right)}^2}{e}^{-\frac{t}{\tau }}+\frac{1}{\sqrt{1+{\left(\omega \tau \right)}^2}}\mathrm{s}\mathrm{i}\mathrm{n}\left\{\omega t+{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(-\omega \tau \right)\right\},\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(t\ge 0\right)\end{array}\end{array}\end{array}$$

上記の右辺第 1 項は t → ∞ で 0 に収束する指数的減衰を，右辺第 2 項は正弦波振動を示している．入力は振幅 1 初期位相 0 の正弦波であるから，右辺第 2 項の正弦波振動の絶対値と偏角は，式 (6‑48) に示した 1 次遅れ要素の周波数伝達関数の絶対値と偏角と各々一致する．

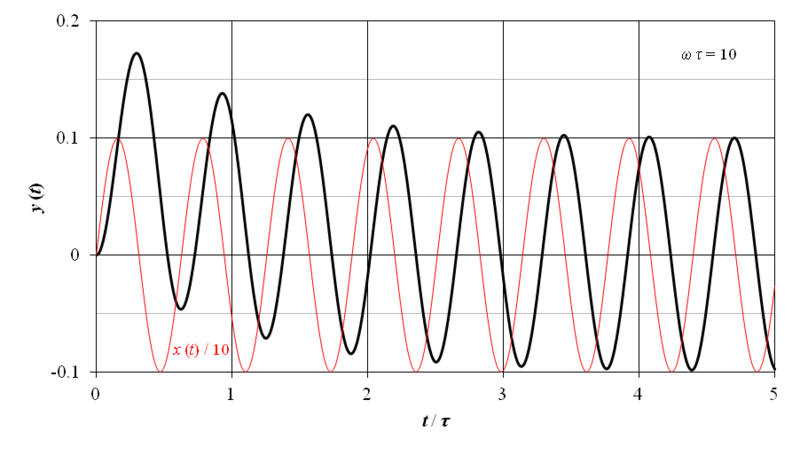
ω τ = 10 における，上記の 1 次遅れ要素の正弦波応答を図7‑3に示す．横軸の時間は t / τ として正規化されている．また，図の赤線は正弦波入力を示しており，正弦波応答と視覚的に比較するために振幅を 1/10 に縮小して表示してある．

図7-3: 1 次遅れ要素の正弦波応答．

7.4. 2 次遅れ要素のインディシャル応答 (単位ステップ応答)

以下の伝達関数で表される 2 次遅れ要素のインディシャル応答を示す．ここで，ω₀ は無減衰固有角周波数，ζ は減衰比とする．

$$\begin{array}{}\text{(7-19)}& G\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{{{\omega }_0}^2}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\end{array}$$

入力及び出力の原関数を各々 x (t), y (t)，これらの像関数を各々 X (s), Y (s) とすると，入力は単位ステップ関数 x (t) = u (t), X (s) = 1 / s であるから，出力 y (t) のラプラス変換 Y (s) は以下で与えられる．

$$\begin{array}{}\text{(7-20)}& Y\left(s\right)=\frac{1}{s}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{{{\omega }_0}^2}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\end{array}$$

ζ > 1 の場合

G (s) の極は実数で単極となるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-21)}& \begin{array}{}\begin{array}{r}Y\left(s\right)\\ \\ \end{array}\begin{array}{l}=\frac{1}{s}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{{{\omega }_0}^2}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\\ =\frac{1}{s}\frac{{{\omega }_0}^2}{\left\{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)\right\}\left\{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)\right\}}\\ =\frac{k_1}{s}+\frac{k_2}{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)}+\frac{k_3}{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)}\end{array}\end{array}\end{array}$$

留数定理より k₁, k₂, k₃ は以下で与えられる (式の展開は省略)．

$$\begin{array}{}\text{(7-22)}& \begin{array}{}\begin{array}{c}{k}_1=\underset{s\to 0}{\lim }<mspace\; width="0.1em"></mspace>sY\left(s\right)=1\\ k_2=\underset{s\to {-\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)}{\lim }<mspace\; width="0.1em"></mspace>\left\{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)\right\}Y\left(s\right)=-\frac{\zeta +\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\\ k_3=\underset{s\to {-\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)}{\lim }<mspace\; width="0.1em"></mspace>\left\{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)\right\}Y\left(s\right)=\frac{\zeta -\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-23)}& Y\left(s\right)=\frac{1}{s}-\frac{\zeta +\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)}+\frac{\zeta -\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)}\end{array}$$

表5‑1 によるラプラス逆変換から，出力 y (t), (t ≥ 0) は以下で与えられる．

$$\begin{array}{}\text{(7-24)}& y\left(t\right)=1-\frac{\zeta +\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}{e}^{-{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)t}+\frac{\zeta -\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}{e}^{-{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)t}\mathrm{<mspace\; width="0.1em"></mspace>}\end{array}$$

ζ = 1 の場合

G (s) の極は実数で重極となるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-25)}& Y\left(s\right)=\frac{1}{s}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{{{\omega }_0}^2}{{\left(s+{\omega }_0\right)}^2}=\frac{k_1}{s}+\frac{k_2}{{\left(s+{\omega }_0\right)}^2}+\frac{k_3}{s+{\omega }_0}\end{array}$$

留数定理より k₁, k₂, k₃ は以下で与えられる．

$$\begin{array}{}\text{(7-26)}& \begin{array}{}\begin{array}{c}{k}_1=\underset{s\to 0}{\lim }<mspace\; width="0.1em"></mspace>sY\left(s\right)=1\\ k_2=\underset{s\to {-\omega }_0}{\lim }{\left(s+{\omega }_0\right)}^{2}Y\left(s\right)=-{\omega }_0\\ k_3=\underset{s\to {-\omega }_0}{\lim }\frac{d}{ds}{\left(s+{\omega }_0\right)}^{2}Y\left(s\right)=\underset{s\to {-\omega }_0}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{-{{\omega }_0}^2}{s^2}=-1\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-27)}& Y\left(s\right)=\frac{1}{s}-\frac{{\omega }_0}{{\left(s+{\omega }_0\right)}^2}-\frac{1}{s+{\omega }_0}\end{array}$$

表5‑1 によるラプラス逆変換から，出力 y (t), (t ≥ 0) は以下で与えられる．

$$\begin{array}{}\text{(7-28)}& y\left(t\right)=1-{\omega }_{0}t{e}^{-{\omega }_{0}t}-e^{-{\omega }_{0}t}=1-\left(1+{\omega }_{0}t\right)\mathrm{<mspace\; width="0.1em"></mspace>}{e}^{-{\omega }_{0}t}\end{array}$$

ζ < 1 の場合

G (s) の極は複素数となるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-29)}& Y\left(s\right)=\frac{k_1}{s}+\frac{k_{2}s+k_3}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\end{array}$$

留数定理より k₁ は以下で与えられる．

$$\begin{array}{}\text{(7-30)}& k_1=\underset{s\to 0}{\lim }<mspace\; width="0.1em"></mspace>sY\left(s\right)=1\end{array}$$

また，係数比較によりk₂ = −1, k₃ = −2 ζ ω₀ となる．ここで式 (7‑29) の右辺第2項を式 (5‑22) の形式に展開する．

$$\begin{array}{}\text{(7-31)}& \frac{-\left(s+2\zeta {\omega }_0\right)}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}=K_1\frac{s-\sigma }{{\left(s-\sigma \right)}^2+{\omega }^2}+K_2\frac{\omega }{{\left(s-\sigma \right)}^2+{\omega }^2}\end{array}$$

式 (5‑23) より σ, ω, K₁, K₂ は以下で与えられる．

$$\begin{array}{}\text{(7-32)}& \begin{array}{}\begin{array}{c}\sigma =-\frac{2\zeta {\omega }_0}{2}=-\zeta {\omega }_0\\ \omega =\frac{\sqrt{4{{\omega }_0}^2-4{\zeta }^2{{\omega }_0}^2}}{2}={\omega }_0\sqrt{1-{\zeta }^2}\\ K_1=-1\\ K_2=\frac{1}{\sqrt{4{{\omega }_0}^2-4{\zeta }^2{{\omega }_0}^2}}\left(-4\zeta {\omega }_0+2\zeta {\omega }_0\right)=-\frac{\zeta }{\sqrt{1-{\zeta }^2}}\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-33)}& Y\left(s\right)=\frac{1}{s}-\frac{s+\zeta {\omega }_0}{{\left(s+\zeta {\omega }_0\right)}^2+{{\omega }_0}^2\left(1-{\zeta }^2\right)}-\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{{\omega }_0\sqrt{1-{\zeta }^2}}{{\left(s+\zeta {\omega }_0\right)}^2+{{\omega }_0}^2\left(1-{\zeta }^2\right)}\end{array}$$

表5‑1 によるラプラス逆変換，及び式 (1‑14) に示した三角関数の合成定理から，出力 y (t), (t ≥ 0) は以下で与えられる．

$$\begin{array}{}\text{(7-34)}& \begin{array}{}\begin{array}{r}y\left(t\right)\\ \end{array}\begin{array}{l}=1-e^{-\zeta {\omega }_{0}t}\cos \left({\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\right)-\frac{\zeta }{\sqrt{1-{\zeta }^2}}{e}^{-\zeta {\omega }_{0}t}\sin \left({\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\right)\\ =1-\frac{e^{-\zeta {\omega }_{0}t}}{\sqrt{1-{\zeta }^2}}\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{s}\mathrm{i}\mathrm{n}\left\{{\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\mathrm{<mspace\; width="0.1em"></mspace>}{+\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{\sqrt{1-{\zeta }^2}}{\zeta }\right)\right\}\end{array}\end{array}\end{array}$$

応答のグラフ

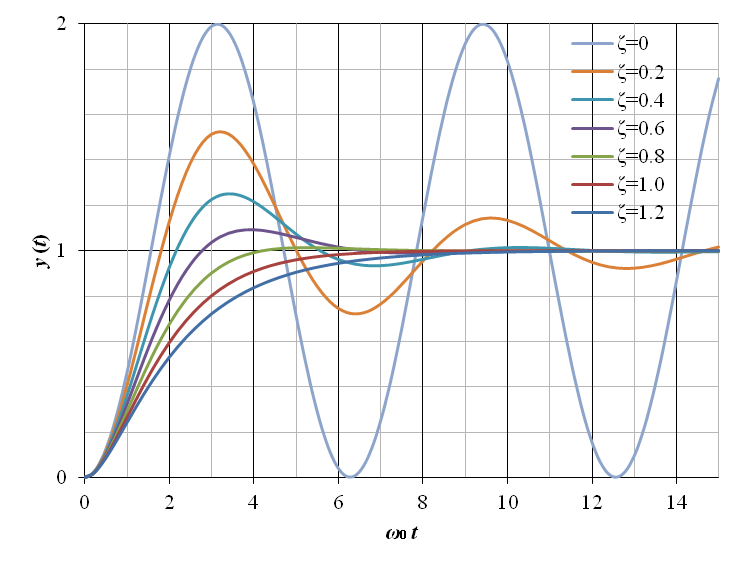
以上の 2 次遅れ要素のインディシャル応答を図7‑4に示す．横軸の時間は ω₀ t として正規化されている．図からも明らかな通り，ζ < 1 の場合は出力 y (t) は振動的となる．尚，振動解析では，ζ > 1 を過減衰，ζ = 1 を臨界減衰，0 < ζ < 1 を減衰振動，ζ = 0 を単振動と呼ぶ．

図7-4: 2 次遅れ要素のインディシャル応答．

以下に続く．

7. 過渡現象 (続き) - 趣味人のブログ