7. 過渡現象 (続き)

7.5. 2 次遅れ要素の正弦波応答

以下の伝達関数で表される 2 次遅れ要素の正弦波応答を示す．ここで，ω₀ は無減衰固有角周波数，ζ は減衰比とする．

$$\begin{array}{}\text{(7-35)}& G\left(s\right)=\frac{Y\left(s\right)}{X\left(s\right)}=\frac{{{\omega }_0}^2}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\end{array}$$

入力及び出力の原関数を各々 x (t), y (t)，これらの像関数を各々 X (s), Y (s) とし，入力を振幅 1 初期位相 0 の正弦波 x (t) = sin (ωt), (t ≥ 0), X (s) = ω / (s² + ω²) とすると，出力 y (t) のラプラス変換 Y (s) は以下で与えられる．

$$\begin{array}{}\text{(7-36)}& Y\left(s\right)=\frac{\omega }{s^2+{\omega }^2}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{{{\omega }_0}^2}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\end{array}$$

議論を簡略化するために，以下 ζ < 1 の場合の解のみを求める．この場合，Y (s) の極は全て複素数となるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-37)}& Y\left(s\right)=\frac{k_{1}s+k_2}{s^2+{\omega }^2}+\frac{k_{3}s+k_4}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\end{array}$$

留数定理より k₁, k₂ は以下で与えられる．

$$\begin{array}{}\text{(7-38)}& \begin{array}{c}\begin{array}{r}\underset{s\to j\omega }{\mathrm{l}\mathrm{i}\mathrm{m}}\left(k_{1}s+k_2\right)\\ \\ \\ \end{array}\begin{array}{l}=k_2+j\omega k_1\\ =\underset{s\to \mathit{j\omega }}{\lim }\left(s^2+{\omega }^2\right)Y\left(s\right)\\ =\underset{s\to j\omega }{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\omega {{\omega }_0}^2}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\\ =\frac{\omega \left[\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}-j2\zeta \frac{\omega }{{\omega }_0}\right]}{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}\end{array}\\ \therefore k_1=\frac{-2\zeta \frac{\omega }{{\omega }_0}}{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}\\ \therefore k_2=\frac{\omega \left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}\end{array}\end{array}$$

また，係数比較により k₃, k₄ は以下で与えられる (式の展開は省略)．

$$\begin{array}{}\text{(7-39)}& \begin{array}{}\begin{array}{c}{k}_3=-k_1=\frac{2\zeta \frac{\omega }{{\omega }_0}}{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}\\ k_4=\frac{4{\zeta }^2\omega -\omega \left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}\end{array}\end{array}\end{array}$$

ここで式 (7-37) の右辺第 2 項を式 (5-22) の形式に展開する．

$$\begin{array}{}\text{(7-40)}& \frac{k_{3}s+k_4}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}=K_1\frac{s-\sigma }{{\left(s-\sigma \right)}^2+{{\omega }_1}^2}+K_2\frac{{\omega }_1}{{\left(s-\sigma \right)}^2+{{\omega }_1}^2}\end{array}$$

式 (5‑23) より σ, ω₁, K₁, K₂ は以下で与えられる．

$$\begin{array}{}\text{(7-41)}& \begin{array}{}\begin{array}{c}\sigma =-\frac{2\zeta {\omega }_0}{2}=-\zeta {\omega }_0\\ {\omega }_1=\frac{\sqrt{4{{\omega }_0}^2-4{\zeta }^2{{\omega }_0}^2}}{2}={\omega }_0\sqrt{1-{\zeta }^2}\\ K_1=k_3=\frac{2\zeta \frac{\omega }{{\omega }_0}}{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}\\ K_2=\frac{1}{\sqrt{1-{\zeta }^2}}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{\frac{\omega }{{\omega }_0}\left[{2\zeta }^2-\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}\right]}{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-42)}& Y\left(s\right)=K_2\frac{{\omega }_0\sqrt{1-{\zeta }^2}}{{\left(s+\zeta {\omega }_0\right)}^2+{{\omega }_0}^2\left(1-{\zeta }^2\right)}+K_1\frac{s+\zeta {\omega }_0}{{\left(s+\zeta {\omega }_0\right)}^2+{{\omega }_0}^2\left(1-{\zeta }^2\right)}+\frac{k_2}{\omega }\mathrm{<mspace\; width="0.1em"></mspace>}\frac{\omega }{s^2+{\omega }^2}+k_1\mathrm{<mspace\; width="0.1em"></mspace>}\frac{s}{s^2+{\omega }^2}\end{array}$$

表5‑1 によるラプラス逆変換，及び式 (1‑14) に示した三角関数の合成定理から，出力 y (t), (t ≥ 0) は以下で与えられる (式の展開は省略)．

$$\begin{array}{}\text{(7-43)}& \begin{array}{c}\begin{array}{r}y\left(t\right)\\ \end{array}\begin{array}{l}=e^{-\zeta {\omega }_{0}t}\left\{K_2\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\mathrm{<mspace\; width="0.1em"></mspace>}\right)+K_1\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\mathrm{<mspace\; width="0.1em"></mspace>}\right)\right\}+\frac{k_2}{\omega }\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)+k_1\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{c}\mathrm{o}\mathrm{s}\left(\omega t\right)\\ =\frac{\mathrm{<mspace\; width="0.1em"></mspace>}\frac{\frac{\omega }{{\omega }_0}{e}^{-\zeta {\omega }_{0}t}}{\sqrt{1-{\zeta }^2}}\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t+\theta \right)+\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t+\phi \right)}{\sqrt{{\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}^2+{\left(2\zeta \frac{\omega }{{\omega }_0}\right)}^2}}\end{array}\\ {\theta =\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{2\zeta \sqrt{1-{\zeta }^2}}{{2\zeta }^2-\left\{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2\right\}}\right),\mathrm{<mspace\; width="0.5em"></mspace>}\mathrm{<mspace\; width="0.5em"></mspace>}{\phi =\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{-2\zeta \frac{\omega }{{\omega }_0}}{1-{\left(\frac{\omega }{{\omega }_0}\right)}^2}\right)\end{array}\end{array}$$

y (t) の右辺第 1 項は，角周波数が無減衰固有角周波数 ω₀ と減衰比 ζ に起因し，かつ t → ∞ で 0 に収束する指数的減衰振動を，右辺第 2 項は角周波数が ω となる入力に起因する定常的な正弦波振動を示している．入力は振幅 1 初期位相 0 の正弦波であるから，右辺第 2 項の正弦波振動の絶対値と偏角は，式 (6‑52) に示した 2 次遅れ要素の周波数伝達関数の絶対値と偏角と各々一致する．

ζ = 0.15, ω / ω₀ = 1.8 における 2 次遅れ要素の正弦波応答を図7‑5に示す．横軸の時間は ω₀ t として正規化されている．図の赤線は上記の指数的減衰振動を，青線は正弦波振動を示している．

図7-5: 2 次遅れ要素の正弦波応答．

7.6. 1 次遅れ要素の零入力応答

図7‑6に示す，抵抗値が R [Ω] の抵抗，及びキャパシタンスが C [F] のコンデンサから成るローパスフィルタの零入力応答を求める．ここで，入力電圧を 0 [V]，即ち x (t) = 0，出力電圧を y (t) [V] とする．また，t = 0 の初期状態においてコンデンサに電荷が蓄えられており，その際の出力電圧を y (0) = y₀ [V] とする．

図7-6: ローパスフィルタ．

式 (6-8) より，上記の回路の入力電圧，出力電圧の関係は以下の定数係数線形常微分方程式で与えられる．

$$\begin{array}{}\text{(7-44)}& CR{\mathrm{<mspace\; width="0.1em"></mspace>}y}^{\text{'}}\left(t\right)+y\left(t\right)=\mathrm{<mspace\; width="0.1em"></mspace>}x\left(t\right)\end{array}$$

上記のラプラス変換を以下に示す．

$$\begin{array}{}\text{(7-45)}& CR\mathrm{<mspace\; width="0.1em"></mspace>}\left\{sY\left(s\right)-y\left(0\right)\right\}+Y\left(s\right)=\mathrm{<mspace\; width="0.1em"></mspace>}X\left(s\right)\end{array}$$

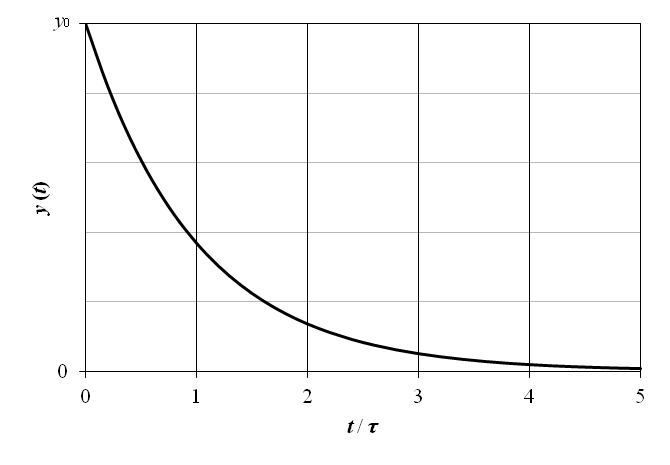
x (t) = 0, y (0) = y₀ であるから，出力電圧 y (t) の像関数 Y (s) は以下となる．ここで τ = CR とする．

$$\begin{array}{}\text{(7-46)}& Y\left(s\right)=\mathrm{<mspace\; width="0.1em"></mspace>}\frac{CR{y}_0}{CRs+1}=\mathrm{<mspace\; width="0.1em"></mspace>}\frac{\tau y_0}{\tau s+1}=\frac{y_0}{s+{\tau }^{-1}}\end{array}$$

表5‑1 によるラプラス逆変換から，出力 y (t) は以下で与えられる．

$$\begin{array}{}\text{(7-47)}& y\left(t\right)=\mathrm{<mspace\; width="0.1em"></mspace>}{y}_0{e}^{-\frac{t}{\tau }},\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(t\ge 0\right)\end{array}$$

上記の 1 次遅れ要素の零入力応答を図7‑7 に示す．横軸の時間は t / τ として正規化されている．

図7-7: 1 次遅れ要素の零入力応答．

7.7. 2 次遅れ要素の零入力応答

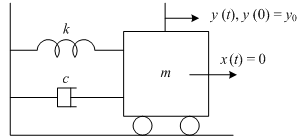
図7‑8に示す，ばね定数が k [N/m] のバネ，質量が m [Kg] のマス，減衰係数が c [Ns/m] のダンパから成るバネマスダンパ系の零入力応答を求める．ここで，入力としての外力を 0 [N]，即ち x (t) = 0，出力を y (t) [m] の変位とし，t = 0 の初期状態において出力に y (0) = y₀ [m] の変位が生じている際の零入力応答を求める．

図7-8: バネマスダンパ系．

上記の運動方程式を以下に示す．

$$\begin{array}{}\text{(7-48)}& m\mathrm{<mspace\; width="0.1em"></mspace>}{y}^{\text{'}\text{'}}\left(t\right)+c{\mathrm{<mspace\; width="0.1em"></mspace>}y}^{\text{'}}\left(t\right)+k\mathrm{<mspace\; width="0.1em"></mspace>}y\left(t\right)=\mathrm{<mspace\; width="0.1em"></mspace>}x\left(t\right)\end{array}$$

上記のラプラス変換を以下に示す．

$$\begin{array}{}\text{(7-49)}& m\mathrm{<mspace\; width="0.1em"></mspace>}\left\{\mathrm{<mspace\; width="0.1em"></mspace>}{s}^{2}Y\left(s\right)-s\mathrm{<mspace\; width="0.1em"></mspace>}y\left(0\right)-{\mathrm{<mspace\; width="0.1em"></mspace>}y}^{\text{'}}\left(0\right)\right\}+c\mathrm{<mspace\; width="0.1em"></mspace>}\left\{sY\left(s\right)-y\left(0\right)\right\}+k\mathrm{<mspace\; width="0.1em"></mspace>}Y\left(s\right)=\mathrm{<mspace\; width="0.1em"></mspace>}X\left(s\right)\end{array}$$

x (t) = 0，かつ初期条件は y (0) = y₀, y' (0) = 0 であるから，変位 y (t) の像関数 Y (s) は以下となる．

$$\begin{array}{}\text{(7-50)}& Y\left(s\right)=\frac{y_0\left(ms+c\right)}{m{s}^2+cs+k}\end{array}$$

ここで上記の式を下記の通り変形する．

$$\begin{array}{}\text{(7-51)}& \begin{array}{}\begin{array}{c}Y\left(s\right)=\frac{y_0\left(s+2\zeta {\omega }_0\right)}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\\ {\omega }_0=\sqrt{\frac{k}{m}}\\ \zeta =\frac{c}{2\sqrt{mk}}\end{array}\end{array}\end{array}$$

ζ > 1 の場合

Y (s) の極は実数で単極となるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-52)}& \begin{array}{}\begin{array}{r}Y\left(s\right)\\ \\ \end{array}\begin{array}{l}=\mathrm{<mspace\; width="0.1em"></mspace>}\frac{y_0\left(s+2\zeta {\omega }_0\right)}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}\\ =\frac{y_0\left(s+2\zeta {\omega }_0\right)}{\left\{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)\right\}\left\{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)\right\}}\\ =\frac{k_1}{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)}+\frac{k_2}{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)}\end{array}\end{array}\end{array}$$

留数定理より k₁, k₂ は以下で与えられる (式の展開は省略)．

$$\begin{array}{}\text{(7-53)}& \begin{array}{}\begin{array}{c}{k}_1=\underset{s\to {-\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)}{\lim }<mspace\; width="0.1em"></mspace>\left\{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)\right\}Y\left(s\right)=y_0\frac{\zeta +\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\\ k_2=\underset{s\to {-\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)}{\lim }<mspace\; width="0.1em"></mspace>\left\{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)\right\}Y\left(s\right)={-y}_0\frac{\zeta -\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-54)}& Y\left(s\right)=y_0\frac{\zeta +\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{s+{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)}-y_0\frac{\zeta -\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{s+{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)}\end{array}$$

表5‑1 によるラプラス逆変換から，出力 y (t), (t ≥ 0) は以下で与えられる．

$$\begin{array}{}\text{(7-55)}& y\left(t\right)=y_0\left(\frac{\zeta +\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}{e}^{-{\omega }_0\left(\zeta -\sqrt{{\zeta }^2-1}\right)t}-\frac{\zeta -\sqrt{{\zeta }^2-1}}{2\sqrt{{\zeta }^2-1}}{e}^{-{\omega }_0\left(\zeta +\sqrt{{\zeta }^2-1}\right)t}\right)\end{array}$$

ζ = 1 の場合

Y (s) の極は実数で重極となるから，Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-56)}& Y\left(s\right)=\mathrm{<mspace\; width="0.1em"></mspace>}\frac{y_0\left(s+2{\omega }_0\right)}{{\left(s+{\omega }_0\right)}^2}=\frac{k_1}{{\left(s+{\omega }_0\right)}^2}+\frac{k_2}{s+{\omega }_0}\end{array}$$

留数定理より k₁, k₂ は以下で与えられる．

$$\begin{array}{}\text{(7-57)}& \begin{array}{}\begin{array}{r}{k}_1=\underset{s\to {-\omega }_0}{\lim }{\left(s+{\omega }_0\right)}^{2}Y\left(s\right)={y_0\mathrm{<mspace\; width="0.1em"></mspace>}\omega }_0\\ k_2=\underset{s\to {-\omega }_0}{\lim }\frac{d}{ds}{\left(s+{\omega }_0\right)}^{2}Y\left(s\right)=y_0\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-58)}& Y\left(s\right)=\frac{{y_0\mathrm{<mspace\; width="0.1em"></mspace>}\omega }_0}{{\left(s+{\omega }_0\right)}^2}+\frac{y_0}{s+{\omega }_0}\end{array}$$

表5‑1 によるラプラス逆変換から，出力 y (t), (t ≥ 0) は以下で与えられる．

$$\begin{array}{}\text{(7-59)}& y\left(t\right)={y_0\omega }_{0}t{e}^{-{\omega }_{0}t}+y_0\mathrm{<mspace\; width="0.1em"></mspace>}{e}^{-{\omega }_{0}t}=y_0\left(1+{\omega }_{0}t\right)\mathrm{<mspace\; width="0.1em"></mspace>}{e}^{-{\omega }_{0}t}\end{array}$$

ζ < 1 の場合

Y (s) の極は複素数となるから，式 (7‑51) を式 (5‑22) の形式に展開する．

$$\begin{array}{}\text{(7-60)}& Y\left(s\right)=\frac{y_0\left(s+2\zeta {\omega }_0\right)}{s^2+2\zeta {\omega }_{0}s+{{\omega }_0}^2}=k_1\frac{s-\sigma }{{\left(s-\sigma \right)}^2+{\omega }^2}+k_2\frac{\omega }{{\left(s-\sigma \right)}^2+{\omega }^2}\end{array}$$

式 (5‑23) より σ, ω, k₁, k₂ は以下で与えられる．

$$\begin{array}{}\text{(7-61)}& \begin{array}{}\begin{array}{c}\sigma =-\frac{2\zeta {\omega }_0}{2}=-\zeta {\omega }_0\\ \omega =\frac{\sqrt{4{{\omega }_0}^2-4{\zeta }^2{{\omega }_0}^2}}{2}={\omega }_0\sqrt{1-{\zeta }^2}\\ K_1=y_0\\ K_2=\frac{y_0}{\sqrt{4{{\omega }_0}^2-4{\zeta }^2{{\omega }_0}^2}}\left(4\zeta {\omega }_0-2\zeta {\omega }_0\right)=y_0\frac{\zeta }{\sqrt{1-{\zeta }^2}}\end{array}\end{array}\end{array}$$

よって Y (s) は以下の部分分数に展開される．

$$\begin{array}{}\text{(7-62)}& Y\left(s\right)=y_0\left\{\frac{s+\zeta {\omega }_0}{{\left(s+\zeta {\omega }_0\right)}^2+{{\omega }_0}^2\left(1-{\zeta }^2\right)}+\frac{\zeta }{\sqrt{1-{\zeta }^2}}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{{\omega }_0\sqrt{1-{\zeta }^2}}{{\left(s+\zeta {\omega }_0\right)}^2+{{\omega }_0}^2\left(1-{\zeta }^2\right)}\right\}\end{array}$$

表5‑1 によるラプラス逆変換，及び式 (1‑14) に示した三角関数の合成定理から，出力 y (t), (t ≥ 0) は以下で与えられる．

$$\begin{array}{}\text{(7-63)}& \begin{array}{}\begin{array}{r}y\left(t\right)\\ \end{array}\begin{array}{l}=y_0\left\{e^{-\zeta {\omega }_{0}t}\cos <mspace\; width="0.1em"></mspace>\left({\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\right)+\frac{\zeta }{\sqrt{1-{\zeta }^2}}{e}^{-\zeta {\omega }_{0}t}\sin <mspace\; width="0.1em"></mspace>\left({\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\right)\right\}\\ =y_0\frac{e^{-\zeta {\omega }_{0}t}}{\sqrt{1-{\zeta }^2}}\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{s}\mathrm{i}\mathrm{n}\left\{{\omega }_0\sqrt{1-{\zeta }^2}\mathrm{<mspace\; width="0.1em"></mspace>}t\mathrm{<mspace\; width="0.1em"></mspace>}{+\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{\sqrt{1-{\zeta }^2}}{\zeta }\right)\right\}\end{array}\end{array}\end{array}$$

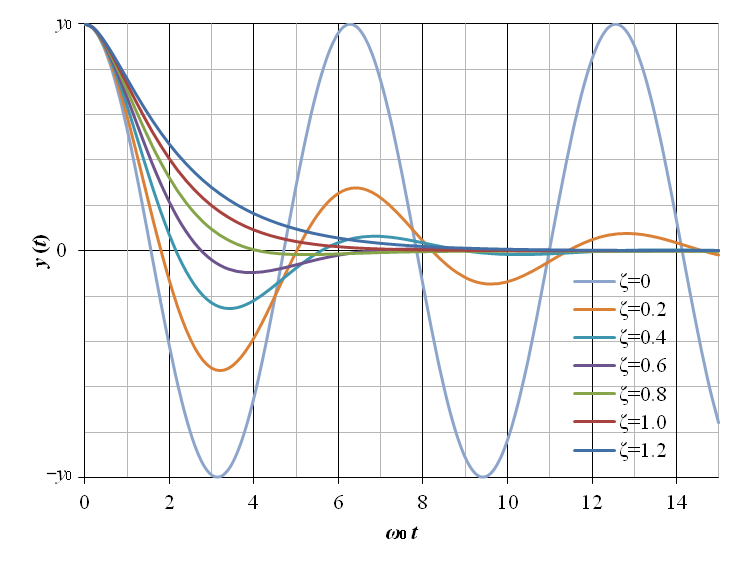
応答のグラフ

以上の 2 次遅れ要素の零入力応答を図7‑9に示す．横軸の時間は ω₀ t として正規化されている．

Note: 振動解析では，上記の様に外力が無い状態における振動を自由振動 (自由応答) と言う．

図7-9: 2 次遅れ要素の零入力応答．

7.8. 1 次遅れ要素のインディシャル応答 (初期条件がある場合)

図7‑10に示す，抵抗値が R [Ω] の抵抗，及びキャパシタンスが C [F] のコンデンサから成るローパスフィルタのインディシャル応答を求める．入出力電圧を各々 x (t), y (t) [V]，これらの像関数を各々 X (s), Y (s) とする．また，t = 0 の初期状態においてコンデンサに電荷が蓄えられており，その際の出力電圧を y (0) = y₀ [V] とする．

図7-10: ローパスフィルタ．

式 (6-8) より，上記の回路の入力電圧，出力電圧の関係は以下の定数係数線形常微分方程式で与えられる．

$$\begin{array}{}\text{(7-64)}& CR{\mathrm{<mspace\; width="0.1em"></mspace>}y}^{\text{'}}\left(t\right)+y\left(t\right)=\mathrm{<mspace\; width="0.1em"></mspace>}x\left(t\right)\end{array}$$

上記のラプラス変換を以下に示す．ここで τ = CR とする．

$$\begin{array}{}\text{(7-65)}& \begin{array}{}\begin{array}{c}CR\mathrm{<mspace\; width="0.1em"></mspace>}\left\{sY\left(s\right)-y\left(0\right)\right\}+Y\left(s\right)=\mathrm{<mspace\; width="0.1em"></mspace>}X\left(s\right)\\ \therefore Y\left(s\right)=\mathrm{<mspace\; width="0.1em"></mspace>}\frac{\tau y\left(0\right)}{\tau s+1}+\frac{X\left(s\right)}{\tau s+1}\end{array}\end{array}\end{array}$$

入力は単位ステップ関数 x (t) = u (t), X (s) = 1 / s，また初期条件は y (0) = y₀ であるから，出力電圧 y (t) の像関数 Y (s) は以下となる．尚，上記の部分分数への分解方法は7.1 及び 7.6 と同じである．

$$\begin{array}{}\text{(7-66)}& Y\left(s\right)=\mathrm{<mspace\; width="0.1em"></mspace>}\frac{{\tau y}_0}{\tau s+1}+\frac{1}{s}\mathrm{<mspace\; width="0.1em"></mspace>}\frac{1}{\tau s+1}=\frac{y_0}{s+{\tau }^{-1}}+\frac{1}{s}-\frac{1}{s+{\tau }^{-1}}\end{array}$$

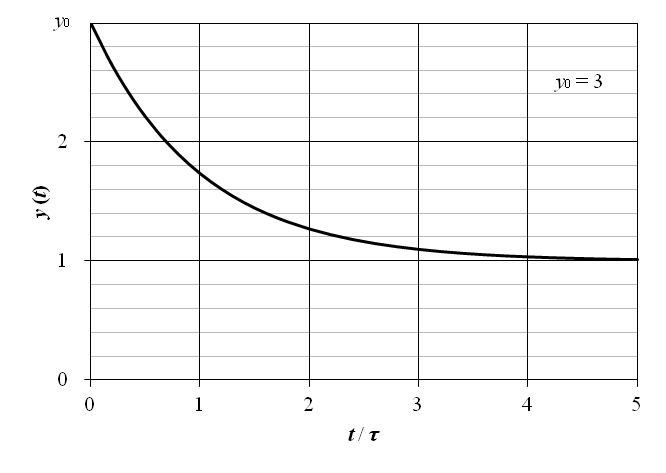
表5‑1 によるラプラス逆変換から，出力 y (t) は以下で与えられる．5.3 に述べた通り，出力 y (t) は零入力応答と零状態応答の重ね合わせとなる．

$$\begin{array}{}\text{(7-67)}& y\left(t\right)=\mathrm{<mspace\; width="0.1em"></mspace>}{y}_0{e}^{-\frac{t}{\tau }}+1-e^{-\frac{t}{\tau }}=1+\left(y_0-1\right)e^{-\frac{t}{\tau }},\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(t\ge 0\right)\end{array}$$

y₀ = 3 における，上記の初期条件がある場合の 1 次遅れ要素のインディシャル応答を図7‑11に示す．横軸の時間は t / τ として正規化されている．

図7-11: 初期条件がある場合の1次遅れ要素のインディシャル応答．

参考: 過渡現象のまとめ

過渡現象とは，図7‑5 に示した 2 次遅れ系の正弦波応答の様に，捉えどころのない予測不可能な振動現象に思えるが，図に示した通り，この振動は単純な指数的減衰振動と正弦波振動の重ね合わせに過ぎない．また，本章の式の展開を子細に確認すれば，類似の展開が多い事に気が付くであろう．特に，7.7 2 次遅れ要素の零入力応答の殆どの数式は，7.4 2 次遅れ要素のインディシャル応答 (単位ステップ応答) のコピペとしか思えず，事実コピペで作成されている．

入力の時間関数 x (t) に対する出力の時間関数 y (t) が，定数係数線形常微分方程式で記述されるシステムの過渡現象 y (t) は，この微分方程式の初期値問題における特殊解で与えられる．これは，式 (5‑12) に示す様に，零入力応答と零状態応答の重ね合わせとなる．5.4 の部分分数への分解方法で述べた通り，これらは式 (5‑12) の各項の分母の次数が何次であろうと，極が実数の場合は 1 次の部分分数，複素数の場合は 2 次の部分部数に分解できる．

ラプラス変換の主要な公式を示した表5‑1 から明らかな通り，これらの部分分数をラプラス逆変換した場合，1 次の部分分数は指数的減衰 (発散)，若しくは定数，2 次の部分分数は指数的減衰振動 (発散振動)，若しくは正弦波となり，これらが n 重解となる場合は t ⁿ 倍される．従って，入出力の関係が定数係数線形常微分方程式で記述されるシステムの過渡現象はこれらの重ね合わせにしかならないのである．