8. フーリエ級数展開とフーリエ変換 (続き)
参考: フーリエ変換と単位インパルス関数
8.2 に示したフーリエ変換の定義では,ごく基本的な関数でもフーリエ変換が収束しない場合がある.例えば f (t) = 1 や周期関数の f (t) の変換が収束しない事は,定義式 (8‑19) から自明である.しかし,5.2に示した単位インパルス関数 (デルタ関数) によって,これらの関数のフーリエ変換を形式的に表示する事が出来る.
単位インパルス関数のフーリエ変換
式 (5‑5) に示した単位インパルス関数 δ (t) の定義より,これのフーリエ変換は以下で与えられる.
上記は,時間関数の単位インパルス関数が,定数の周波数関数,即ち振幅が等しく周波数成分が ∞ までとなる正弦波と直流成分の重ね合わせによって表せる事を示している.上記のフーリエ逆変換は以下で与えられる.
ここで,上記の式の変数を入れ替えると,以下の通り変形できる.
式 (8-27), (8-28) の積分は収束しないが,単位インパルス関数はこれらの式によって形式的に表示する事ができる.これらの怪しさ爆発する式は,単位インパルス関数の積分表示と呼ばれる.
直流成分のフーリエ変換
単位インパルス関数の積分表示より f (t) = A のフーリエ変換は以下で表示する事ができる.
上記のフーリエ逆変換を以下に示す.
上記は,定数の時間関数,即ち直流成分が,周波数関数の単位インパルス関数によって表せる事を示している.これは前に述べた,時間関数の単位インパルス関数が,定数の周波数関数によって表せる事と対称的な関係を示している.
正弦関数,余弦関数のフーリエ変換
単位インパルス関数の積分表示より,f (t) = A sin (ω0t) のフーリエ変換は以下で表示する事ができる.
上記のフーリエ逆変換を以下に示す.
同様に,単位インパルス関数の積分表示より,f (t) = A cos (ω0t) のフーリエ変換は以下で表示する事ができる.
ここで,上記の F (ω0) は以下で与えられる.
上記及び,直流成分,正弦関数,余弦関数のフーリエ変換を表示した式 (8-29), (8-31), (8-33) からも明らかな通り,これらのフーリエ変換には単位インパルス関数が現れる.従って,8.2 に述べた方法では,これらのフーリエ変換から正弦波の振幅や初期位相,直流成分を求める事はできない.勿論,ご都合主義的に,これらの式の単位インパルス関数を無視する事も可能であるが,フーリエ変換の結果に単位インパルス関数を含む項と含まない項が混在した場合の解釈が困難となる.
また,これらの結果に対してパーセバルの定理は成立しないとされている.そもそも,理論上,想像上の関数である単位インパルス関数のエネルギーを論じる事の意味を見い出す事は困難である.結局,単位インパルス関数は理論上,想像上の関数であるため,これが時間関数として現れても,周波数関数として現れても,その意味を正確に議論する事は容易ではない.従って,単位インパルス関数によって,直流成分や周期関数のフーリエ変換が「形式的に表示できるだけ」と考えた方が現実的である.
では,何故この様な無用と思われる議論を述べているかと言うと,9.2 に述べるサンプル値の表現にはこの表示方法が使われている点と,以下の様な議論が可能となる点にある.
単位ステップ関数のフーリエ変換
以下で定義される単位ステップ関数 u (t) のフーリエ変換を求める.
式 (5-8) に示した通り,単位インパルス関数は単位ステップ関数の微分であるから,表8-1 に示したフーリエ変換の微分の定理により,単位ステップ関数のフーリエ変換は以下で表示する事ができる.
以上が,教科書的な単位ステップ関数のフーリエ変換の説明であるが,残念な事に単位ステップ関数は不連続な関数であるから,上記をフーリエ逆変換すると不連続点の u (0) は近似となり,単位ステップ関数に厳密には収束しない.前に述べたフーリエ逆変換の収束の規則から,上記をフーリエ逆変換した関数 uc (t) を以下に示す.
次に,改めて上記の関数 uc (t) のフーリエ変換を求める.これには以下の符号関数 sgn (t) を用いる.
符号関数 sgn (t) のフーリエ変換は以下の通りとなる事が既知である.(以下の導出は工学の範囲を超えるため割愛する).
ここで,関数 uc (t) と符号関数 sgn (t) には以下の関係がある.
よって,フーリエ変換の線形性の定理と,前に述べた f (t) = a のフーリエ変換から,関数 uc (t) のフーリエ変換は以下で表示する事ができる.
上記の πδ (ω) は 1 / 2 の直流成分を表す.従って,式 (8‑36) に示した,単位ステップ関数 u (t) のフーリエ変換には,単位ステップ関数の直流成分が正確に表示されていない事が判る.
余談: ラプラス変換 = フーリエ変換説
一部の教科書に,ラプラス変換において s = jω とすればフーリエ変換となるとの説が見受けられる.おおむね,この説はラプラス変換の積分範囲を −∞ から ∞ とした両側ラプラス変換に基づいている.ラプラス変換の原関数 f (t) の両側ラプラス変換 F (s) の定義を以下に示す.式 (5‑1) に定義したラプラス変換と下記を区別するために,ここでは前者を片側ラプラス変換と呼ぶ.
この説では,上記の両側ラプラス変換において s = jω とすればフーリエ変換の定義式となり,かつ原関数を f (t) = 0, (t < 0) とすれば片側ラプラス変換の定義式と等価となるから,片側ラプラス変換において s = jω とすればフーリエ変換となるとしている.(尚,ここまで丁寧に書かれていない説明が殆どである).
片側ラプラス変換と両側ラプラス変換の定義は似ているため,表5‑1や表5‑2に示した片側ラプラス変換の公式や定理の殆どは両側ラプラス変換においても成立するが,残念ながら成立しない場合もある.定理が異なる例として片側ラプラス変換における微分の定理を以下に示す.
これらから明らかな通り,片側ラプラス変換と異なり,両側ラプラス変換やフーリエ変換における微分の定理には − f (+0) の項が無いため,原関数を f (t) = 0, (t < 0) とする制約は,f (t) の片側ラプラス変換と両側ラプラス変換が等価となる条件としては不十分であり,これに加えて少なくとも f (0) = 0 とする制約が必要となる.即ち,両側ラプラス変換は,片側ラプラス変換と似てはいるが,これを包含するものでは無い.
5.3に述べた通り,片側ラプラス変換によって定数係数線形常微分方程式の初期値問題における特殊解を求める事ができる.この場合,原関数 f (t) の定義域は t ≥ 0 となる制約があるが,任意の初期条件を与える事ができる.一方,4.4に述べた未定係数法と同様に,フーリエ変換によって定数係数線形常微分方程式の非同次方程式の特殊解 (定常解) yp (t) を求める事ができる (これは実質的に未定係数法と同じ解法であり,わざわざフーリエ変換によって解く意味は無いため詳細は割愛する).この場合,未定係数法と同様に,原関数 f (t) の定義域に制約は無く解は初期条件に依存しない.
従って,片側ラプラス変換やフーリエ変換を定数係数線形常微分方程式の解法とした場合,これらは異なる制約条件における異なる問題の解法となるため,単に原関数を f (t) = 0, (t < 0) とし s = jω とすればこれらは等価という説明は著しく正確性を欠く.
多分この説の出処は,伝達関数において s = jω とすれば周波数伝達関数となる事を,ラプラス変換とフーリエ変換の関係として説明したい点にあると推測するが,伝達関数は初期条件が全て 0,即ち f (0) = f ' (0) = ... = 0 を前提としており,この場合は片側ラプラス変換と両側ラプラス変換,即ちフーリエ変換は等価となるため,伝達関数において s = jω とすれば周波数伝達関数となるのである
8. フーリエ級数展開とフーリエ変換
本章はフーリエ級数展開とフーリエ変換について述べる.これらフーリエ解析は振動の分析に適用する事ができ,線形時不変システムより広い分野で利用されているため,非常に多くの教科書がある.このため,本資料では数式の証明や導出は省略し,振動の分析という観点からの解説を行う.尚,フーリエ解析における種々の関係は,以下の f (t) が複素数の場合でも成立するが,その物理的な意味を見い出す事は容易ではないため,本資料では扱わない.
8.1. フーリエ級数展開
周期 2π の周期関数のフーリエ級数展開
f (t) を区間 [−π, π] で定義された周期 2π の周期関数とすると,以下の式に示す通り,f (t) は定数,及び周期 2π / n, (n = 1, 2, 3, ...) の正弦関数,及び余弦関数の和から成るフーリエ級数で表す事ができる.下記の式の ~ は,フーリエ級数が厳密に f (t) に収束する場合と,近似となる場合がある事を示している.
ここで,an 及び bn はフーリエ係数と呼ばれ,以下で与えられる.
以上がフーリエ級数展開の教科書的定義である.ここで,式 (1-14) に示した三角関数の合成定理によって,式 (8-1) は以下の通り変形できる.
即ち,f (t) を時間 [−π, π] で定義された周期 2π の振動における変位とすると,上記は角周波数が n,振幅が An,初期位相が φn, (n = 1, 2, 3, ...) となる正弦波と,直流成分 a0 / 2の重ね合わせで f (t) を表せる事を示している.
式 (8‑2) のフーリエ係数を,以下の式に基づいて,複素フーリエ係数に変換すると,複素フーリエ級数が得られる.
複素フーリエ級数と複素フーリエ係数を以下に示す.これらは,式 (8-1) 及び (8-2) の別表現となる.
以上が,複素フーリエ級数展開の教科書的定義である.ここで,f (t) が実数の場合は cn と c−n は共役複素数の関係となるため,式 (8‑5) は以下の通り変形できる.
ここで,An = | j2cn | = 2 | cn |, φn = Arg ( j2cn ) とすると,上記は更に以下の通り変形できる.
上記の複素フーリエ級数の総和における各項は,式 (2‑27) に示した複素指数関数による正弦波の記述となる.よって,f (t) を時間 [−π, π] で定義された周期 2π の振動における変位とすると,上記は角周波数が n,振幅が An,初期位相が φn, (n = 1, 2, 3, ...) となる正弦波と,直流成分 c0 の重ね合わせで f (t) を表せる事を示している.
Note: 上記の直流成分は c0 となるが,正弦波の振幅は 2 | cn | となる事に注意せよ.フーリエ級数に限らず,フーリエ解析を正弦波と直流成分の重ね合わせとして解釈する場合,直流成分と正弦波は区別して扱わなければならない.
周期 2L の周期関数のフーリエ級数展開
f (t) を区間 [−L, L] で定義された周期 2L の周期関数とすると,以下の式に示す通り,f (t) は定数,及び周期 2L / n, (n = 1, 2, 3, ...) の正弦関数,及び余弦関数の和から成るフーリエ級数で表す事ができる.
フーリエ係数 an 及び bn は以下で与えられる.
また,上記の別表現となる複素フーリエ級数と複素フーリエ係数を以下に示す.
以上の教科書的定義において L = π / ω と置き換えると,f (t) は区間 [−π / ω, π / ω] で定義された周期 2π / ω の周期関数となる.この場合,f (t) を時間 [−π / ω, π / ω] で定義された周期 2π / ω の振動における変位とすると,f (t) は,以下の通り,角周波数が nω,振幅が An,初期位相が φn, (n = 1, 2, 3, ...) となる正弦波と,直流成分 a0 / 2の重ね合わせで表す事ができる.
また,式 (8‑10) の f (t) が実数の場合は cn と c−n は共役複素数の関係となるため,式 (8‑10) の複素フーリエ級数と複素フーリエ係数は以下の通り変形できる.
上記は角周波数が nω,振幅が An,初期位相が φn, (n = 1, 2, 3, ...) となる正弦波と,直流成分 c0 の重ね合わせで f (t) を表せる事を示している.
フーリエ級数の収束
f (t) を区間 [a, b] で定義された周期関数とすると,f (t) が有限個の点を除いて連続であり,かつ全ての不連続点において,左側極限値と右側極限値が存在し,かつ a 及び b において各々左側極限値と右側極限値が存在する場合,f (t) を区分的に連続な関数と言う.また,周期関数 f (t) の導関数 f '(t) が区間 [a, b] において区分的に連続な関数となる場合,f (t) を区分的に滑らかな関数と言う.
区分的に連続,かつ区分的に滑らかな周期関数 f (t) のフーリエ級数の収束を以下に示す.
即ち,フーリエ級数は連続関数となる正弦波,及び直流成分の重ね合わせによって周期関数を表現するものであるため,連続な点は厳密に表現できるが,不連続点は近似となり,これを厳密に表現する事は出来ない.
ギブスの現象
f (t) が以下で与えられる周期 2π の方形波 (矩形波) のフーリエ級数を例に,不連続点におけるフーリエ級数の収束過程を示す.
上記の方形波のフーリエ級数は以下で与えられる.
上記のフーリエ級数の総和を n = 1 から m までの部分和で近似した際のグラフを以下に示す.

図から明らかな通り,m が増大するに伴い,正弦波の重ね合わせは方形波に近づき,f (t) に収束してゆく.但し,不連続点の近傍で振動的な現象が観察される.m を更に増大させ,不連続点の近傍を拡大した図を以下に示す.

図から明らかな通り,不連続点の近傍における振動的な現象は m が増大しても生じる.これはギブスの現象と呼ばれ,不連続点を含む周期関数のフーリエ級数の総和を部分和で近似した場合,不連続点の近傍で必ず生じる事が知られている.尚,不連続点 f (t) 近傍における,振動的な現象によるオーバーシュート,アンダーシュートの振幅は,不連続点の幅 f (t − 0) − f (t + 0) の約 0.09 倍となる.
以上が,ギブスの現象の教科書的説明である.ここで,振動の分析の観点からは,方形波のフーリエ級数の総和を部分和で近似する事は,方形波をローパスフィルタに通す事に等しい.従って,ギブスの現象は,カットオフ周波数を超える周波数成分を全く含まないローパスフィルタのインディシャル応答 (単位ステップ応答) や方形波の応答が,不連続点近傍で振動的となる事を示している.この振動はリップル (リンギング) と呼ばれる.
図6‑10 に示した通り,2 次遅れ要素のゲインは固有振動数 (共振周波数) 近傍で 0 [dB] 以上となるため,7.4 に示した通り,これのインディシャル応答が振動的となる事は直感的に理解できる.しかし,固有振動数を持たないローパスフィルタであっても,インディシャル応答が振動的となる場合がある事に十分留意する必要がある.事実,ローパスフィルタとして基本的な特性のバタワースフィルタは,次数を高くし減衰傾斜を急峻にすると,インディシャル応答や方形波の応答が振動的となり,リップルが生じる事が知られている.
リップルが生じるフィルタは,用途によっては許容されない場合がある.カットオフ周波数を超える周波数成分を全く含まないローパスフィルタは「理想的」フィルタと呼ばれ,またフィルタの減衰傾斜は急峻であるほど良い特性であるとの誤解が多く見受けられるが,過ぎたるは猶及ばざるが如し,その様な特性のフィルタは用途によっては問題を引き起こす可能性がある事に留意する必要がある.
窓関数によるリップルの抑制
リップルは,単純に減衰傾斜を緩やかにすれば抑制する事ができる.上に述べた方形波のフーリエ級数の総和を部分和で近似する場合は,部分和の各項に重み付の係数を乗じる事によってこれを実現できる.この様な重み付の技法は無数に存在するが,その代表的なものとして窓関数がある.最も良く使われる窓関数としてハミング窓を以下に示す.
ここで,w [n] は項 n の重み付の係数,N は項数を示す.上記は,多くの教科書に示されているハミング窓の定義で,n = N / 2 を中心とした項の重み付を高くする場合の定義式となる.
上に述べた,方形波のフーリエ級数の総和を部分和で近似する場合は,n = 0 を周辺の項の重み付を高くする必要があり,この場合のハミング窓の定義式は以下で与えられる.
よって,ハミング窓で重み付された,方形波のフーリエ級数における m 項までの部分和による近似は以下で与えられる.
上記の計算結果のグラフを以下に示す.
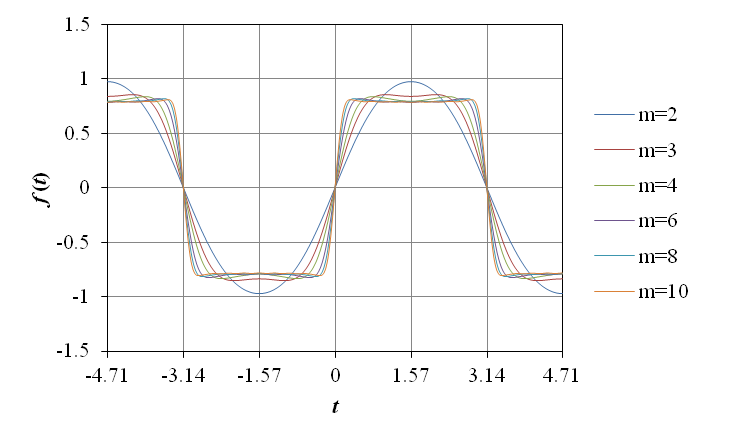
図から明らかな通り,ハミング窓による重み付により減衰傾斜が緩やかとなり,リップルは殆ど生じていない.その反面,重み付の影響により信号の立ち上がり,立下りに要する時間が長くなり,波形の変化が緩やかになっている.
8.2. フーリエ変換
フーリエ変換の定義
周期 2L の周期関数のフーリエ係数,フーリエ級数展開を L→∞ とする事によってフーリエ変換,フーリエ逆変換が得られる.区間 [−∞, ∞] で定義された関数 f (t) のフーリエ変換 F (ω) を以下に示す.
関数 f (t) とフーリエ変換 F (ω) の関係を以下の様に表示する場合もある.
同様に,関数 f (t) は F (ω) のフーリエ逆変換とも呼ばれ,以下の式で表す事ができる.フーリエ級数と同様に,下記の式の ~ は,フーリエ逆変換が厳密に f (t) に収束する場合と,近似となる場合がある事を示している.
上記の関係を以下の様に表示する場合もある.
フーリエ変換,逆変換の定義式は,係数 1 / (2π) を除けば,t と ω を入れ替えただけで,実質的に同じ式となる.
Note: フーリエ変換,逆変換の定義式は分野や文献によって異なる.特に,係数 1 / (2π) を変換,逆変換のどちらの係数とするかに差異が見られる.フーリエ係数との整合性の観点から,係数 1 / (2π) をフーリエ変換の定義式の係数とする場合もある.また,フーリエ変換,逆変換の定義式の対称性,パーセバルの定理によるエネルギーの計算との整合性の観点から,係数 1 / (2π) の平方根を変換,逆変換双方の係数とする場合もある.本資料ではラプラス変換の定義式との整合性の観点から,上記の様に係数 1 / (2π) を逆変換の定義式の係数としている.
以上が,フーリエ変換の教科書的定義である.ここで,f (t) が実数の場合は F (ω) と F (−ω) は共役複素数の関係となるため,フーリエ逆変換の定義式 (8‑21) は以下の通り変形できる.
即ち,f (t) を時間 [−∞, ∞] で定義された振動における変位とすると,上記は角周波数をω,振幅を A (ω),初期位相を φ (ω), (ω > 0) とする正弦波と,直流成分 F (0) / (2π) の重ね合わせで f (t) を表せる事を示している.
Note: 以上述べた通り,フーリエ級数及びフーリエ変換は,ある波形の振動を正弦波の重ね合わせによって表現する際の,各正弦波の振幅,及び初期位相を示している.振動の分析にフーリエ解析を利用する際の目的によっては,角周波数と振幅の関係にしか興味が無い場合もあるが,特定分野の技術者向けの解説書ならいざ知らず,教科書レベルの文献において,初期位相は重要では無いと言った記述が散見されて仰天している.正弦波を合成した際に得られる波形は,各正弦波の振幅と初期位相に依存する.従って,振動を正弦波の重ね合わせによって表現する際に必要となる情報は,各正弦波の角周波数,振幅,及び初期位相となる.
フーリエ逆変換の収束
区間 [−∞, ∞] で定義された関数 f (t) が以下の式を満たす場合,f (t) を絶対積分可能な関数と言う.
関数 f (t) が絶対積分が可能,かつ区分的に連続,区分的に滑らかな場合,関数 f (t) のフーリエ変換 F (ω) が存在する.また,その場合のフーリエ逆変換の収束を以下に示す.
即ち,フーリエ級数と同様に,フーリエ逆変換も,連続な点は厳密に表現できるが,不連続点は元の関数の近似となり,これを厳密に表現する事は出来ない.
フーリエ変換の定理
フーリエ変換の主要な定理を以下に示す.
| 線 形 性 | |
| 縮 尺 | |
| 対 称 性 | |
| 微 分 | |
| 畳み込み | |
| パーセバルの定理 | |
| 時間軸のシフト | |
| 周波数軸のシフト |
以下に続く.
7. 過渡現象 (続き)
- 7.5. 2 次遅れ要素の正弦波応答
- 7.6. 1 次遅れ要素の零入力応答
- 7.7. 2 次遅れ要素の零入力応答
- 7.8. 1 次遅れ要素のインディシャル応答 (初期条件がある場合)
- 参考: 過渡現象のまとめ
7.5. 2 次遅れ要素の正弦波応答
以下の伝達関数で表される 2 次遅れ要素の正弦波応答を示す.ここで,ω0 は無減衰固有角周波数,ζ は減衰比とする.
入力及び出力の原関数を各々 x (t), y (t),これらの像関数を各々 X (s), Y (s) とし,入力を振幅 1 初期位相 0 の正弦波 x (t) = sin (ωt), (t ≥ 0), X (s) = ω / (s2 + ω2) とすると,出力 y (t) のラプラス変換 Y (s) は以下で与えられる.
議論を簡略化するために,以下 ζ < 1 の場合の解のみを求める.この場合,Y (s) の極は全て複素数となるから,Y (s) は以下の部分分数に展開される.
留数定理より k1, k2 は以下で与えられる.
また,係数比較により k3, k4 は以下で与えられる (式の展開は省略).
ここで式 (7-37) の右辺第 2 項を式 (5-22) の形式に展開する.
式 (5‑23) より σ, ω1, K1, K2 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
表5‑1 によるラプラス逆変換,及び式 (1‑14) に示した三角関数の合成定理から,出力 y (t), (t ≥ 0) は以下で与えられる (式の展開は省略).
y (t) の右辺第 1 項は,角周波数が無減衰固有角周波数 ω0 と減衰比 ζ に起因し,かつ t → ∞ で 0 に収束する指数的減衰振動を,右辺第 2 項は角周波数が ω となる入力に起因する定常的な正弦波振動を示している.入力は振幅 1 初期位相 0 の正弦波であるから,右辺第 2 項の正弦波振動の絶対値と偏角は,式 (6‑52) に示した 2 次遅れ要素の周波数伝達関数の絶対値と偏角と各々一致する.
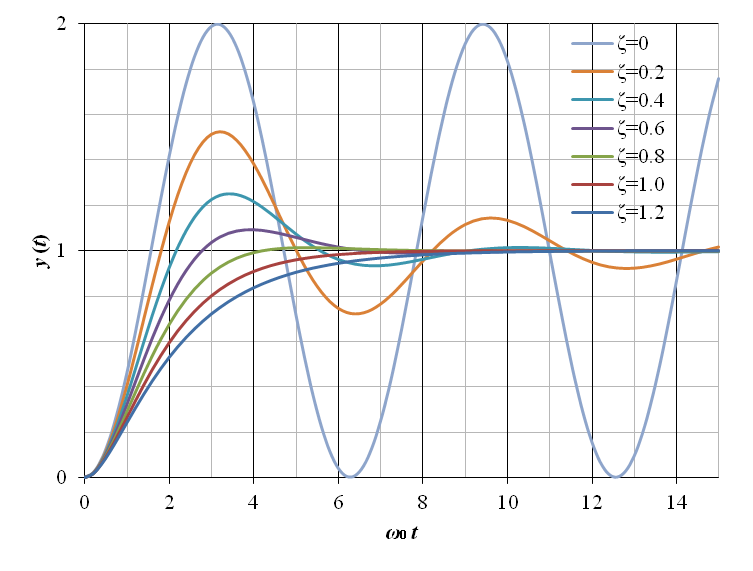
ζ = 0.15, ω / ω0 = 1.8 における 2 次遅れ要素の正弦波応答を図7‑5に示す.横軸の時間は ω0 t として正規化されている.図の赤線は上記の指数的減衰振動を,青線は正弦波振動を示している.

7.6. 1 次遅れ要素の零入力応答
図7‑6に示す,抵抗値が R [Ω] の抵抗,及びキャパシタンスが C [F] のコンデンサから成るローパスフィルタの零入力応答を求める.ここで,入力電圧を 0 [V],即ち x (t) = 0,出力電圧を y (t) [V] とする.また,t = 0 の初期状態においてコンデンサに電荷が蓄えられており,その際の出力電圧を y (0) = y0 [V] とする.

式 (6-8) より,上記の回路の入力電圧,出力電圧の関係は以下の定数係数線形常微分方程式で与えられる.
上記のラプラス変換を以下に示す.
x (t) = 0, y (0) = y0 であるから,出力電圧 y (t) の像関数 Y (s) は以下となる.ここで τ = CR とする.
表5‑1 によるラプラス逆変換から,出力 y (t) は以下で与えられる.
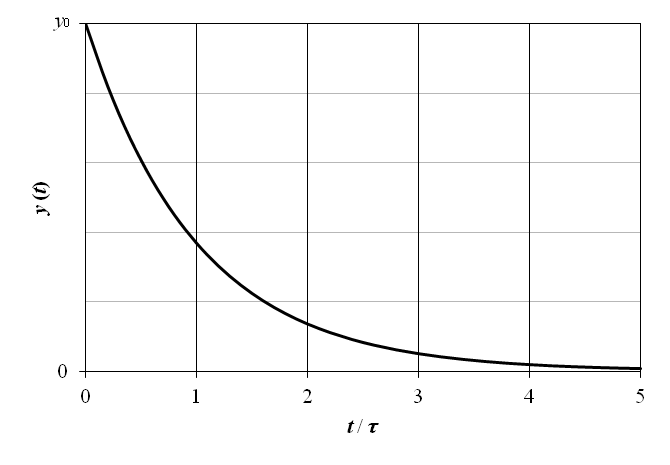
上記の 1 次遅れ要素の零入力応答を図7‑7 に示す.横軸の時間は t / τ として正規化されている.
7.7. 2 次遅れ要素の零入力応答
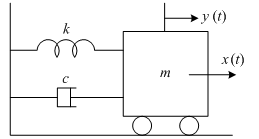
図7‑8に示す,ばね定数が k [N/m] のバネ,質量が m [Kg] のマス,減衰係数が c [Ns/m] のダンパから成るバネマスダンパ系の零入力応答を求める.ここで,入力としての外力を 0 [N],即ち x (t) = 0,出力を y (t) [m] の変位とし,t = 0 の初期状態において出力に y (0) = y0 [m] の変位が生じている際の零入力応答を求める.
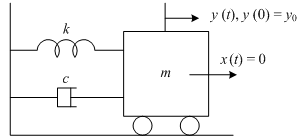
上記の運動方程式を以下に示す.
上記のラプラス変換を以下に示す.
x (t) = 0,かつ初期条件は y (0) = y0, y' (0) = 0 であるから,変位 y (t) の像関数 Y (s) は以下となる.
ここで上記の式を下記の通り変形する.
ζ > 1 の場合
Y (s) の極は実数で単極となるから,Y (s) は以下の部分分数に展開される.
留数定理より k1, k2 は以下で与えられる (式の展開は省略).
よって Y (s) は以下の部分分数に展開される.
表5‑1 によるラプラス逆変換から,出力 y (t), (t ≥ 0) は以下で与えられる.
ζ = 1 の場合
Y (s) の極は実数で重極となるから,Y (s) は以下の部分分数に展開される.
留数定理より k1, k2 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
表5‑1 によるラプラス逆変換から,出力 y (t), (t ≥ 0) は以下で与えられる.
ζ < 1 の場合
Y (s) の極は複素数となるから,式 (7‑51) を式 (5‑22) の形式に展開する.
式 (5‑23) より σ, ω, k1, k2 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
表5‑1 によるラプラス逆変換,及び式 (1‑14) に示した三角関数の合成定理から,出力 y (t), (t ≥ 0) は以下で与えられる.
応答のグラフ
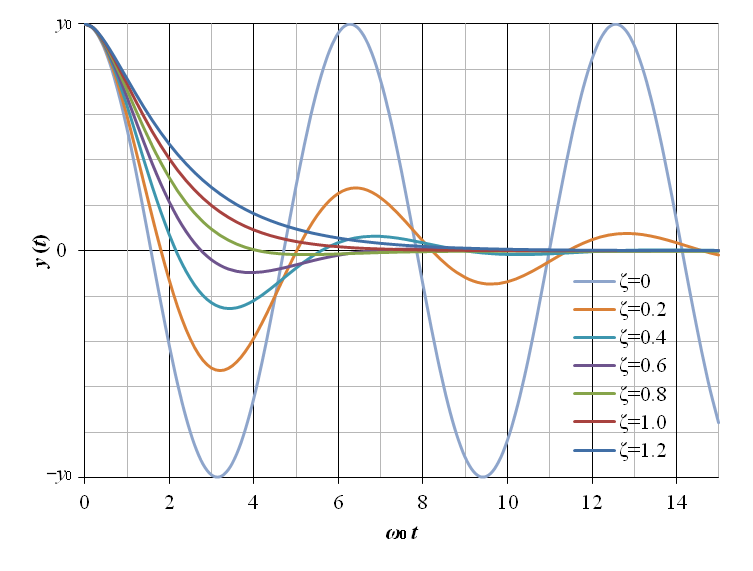
以上の 2 次遅れ要素の零入力応答を図7‑9に示す.横軸の時間は ω0 t として正規化されている.
Note: 振動解析では,上記の様に外力が無い状態における振動を自由振動 (自由応答) と言う.
7.8. 1 次遅れ要素のインディシャル応答 (初期条件がある場合)
図7‑10に示す,抵抗値が R [Ω] の抵抗,及びキャパシタンスが C [F] のコンデンサから成るローパスフィルタのインディシャル応答を求める.入出力電圧を各々 x (t), y (t) [V],これらの像関数を各々 X (s), Y (s) とする.また,t = 0 の初期状態においてコンデンサに電荷が蓄えられており,その際の出力電圧を y (0) = y0 [V] とする.

式 (6-8) より,上記の回路の入力電圧,出力電圧の関係は以下の定数係数線形常微分方程式で与えられる.
上記のラプラス変換を以下に示す.ここで τ = CR とする.
入力は単位ステップ関数 x (t) = u (t), X (s) = 1 / s,また初期条件は y (0) = y0 であるから,出力電圧 y (t) の像関数 Y (s) は以下となる.尚,上記の部分分数への分解方法は7.1 及び 7.6 と同じである.
表5‑1 によるラプラス逆変換から,出力 y (t) は以下で与えられる.5.3 に述べた通り,出力 y (t) は零入力応答と零状態応答の重ね合わせとなる.
y0 = 3 における,上記の初期条件がある場合の 1 次遅れ要素のインディシャル応答を図7‑11に示す.横軸の時間は t / τ として正規化されている.
参考: 過渡現象のまとめ
過渡現象とは,図7‑5 に示した 2 次遅れ系の正弦波応答の様に,捉えどころのない予測不可能な振動現象に思えるが,図に示した通り,この振動は単純な指数的減衰振動と正弦波振動の重ね合わせに過ぎない.また,本章の式の展開を子細に確認すれば,類似の展開が多い事に気が付くであろう.特に,7.7 2 次遅れ要素の零入力応答の殆どの数式は,7.4 2 次遅れ要素のインディシャル応答 (単位ステップ応答) のコピペとしか思えず,事実コピペで作成されている.
入力の時間関数 x (t) に対する出力の時間関数 y (t) が,定数係数線形常微分方程式で記述されるシステムの過渡現象 y (t) は,この微分方程式の初期値問題における特殊解で与えられる.これは,式 (5‑12) に示す様に,零入力応答と零状態応答の重ね合わせとなる.5.4 の部分分数への分解方法で述べた通り,これらは式 (5‑12) の各項の分母の次数が何次であろうと,極が実数の場合は 1 次の部分分数,複素数の場合は 2 次の部分部数に分解できる.
ラプラス変換の主要な公式を示した表5‑1 から明らかな通り,これらの部分分数をラプラス逆変換した場合,1 次の部分分数は指数的減衰 (発散),若しくは定数,2 次の部分分数は指数的減衰振動 (発散振動),若しくは正弦波となり,これらが n 重解となる場合は t n 倍される.従って,入出力の関係が定数係数線形常微分方程式で記述されるシステムの過渡現象はこれらの重ね合わせにしかならないのである.
7. 過渡現象
本章では,初期条件が 0 であり,伝達関数が定義される 1 次遅れ要素のインディシャル応答,ランプ応答,正弦波応答,2 次遅れ要素のインディシャル応答,正弦波応答を示す.次に,初期条件が 0 とならず伝達関数が定義されない 1 次遅れ要素,2 次遅れ要素の零入力応答を示す.最後に,同様に初期条件が 0 とならず伝達関数が定義されない 1 次遅れ要素のインディシャル応答を示し,初期条件,入力が共にある場合の出力は,これらの零入力応答と零状態応答の重ね合わせとなる事を述べる.
- 7.1. 1 次遅れ要素のインディシャル応答 (単位ステップ応答)
- 7.2. 1 次遅れ要素のランプ応答
- 7.3. 1 次遅れ要素の正弦波応答
- 7.4. 2 次遅れ要素のインディシャル応答 (単位ステップ応答)
7.1. 1 次遅れ要素のインディシャル応答 (単位ステップ応答)
以下の伝達関数で表される 1 次遅れ要素のインディシャル応答を示す.ここで,τ は時定数とする.
入力及び出力の原関数を各々 x (t), y (t),これらの像関数を各々 X (s), Y (s) とすると,入力は単位ステップ関数 x (t) = u (t), X (s) = 1 / s であるから,出力 y (t) のラプラス変換 Y (s) は以下で与えられる.
ここで,Y (s) を以下の部分分数に展開する.
留数定理より k1, k2 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
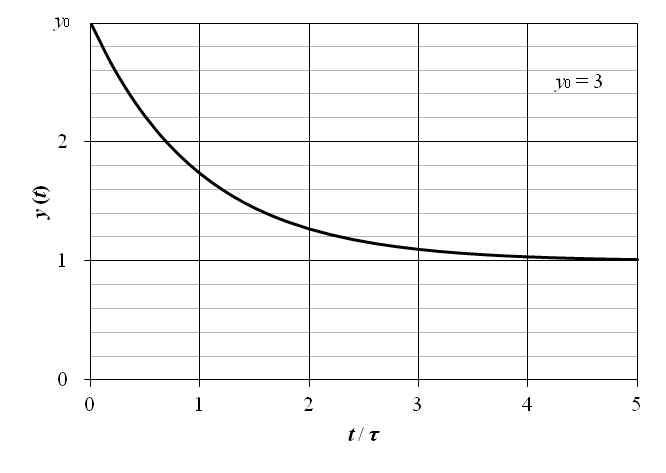
表5‑1 によるラプラス逆変換から,出力 y (t) は以下で与えられる.
上記の 1 次遅れ要素のインディシャル応答を図7‑1 に示す.横軸の時間は t / τ として正規化されている.図から明らかな通り,出力 y (t) の立ち上がりに要する時間は,時定数 τ に反比例する.即ち時定数が小さいほど立ち上がり時間は早くなる.また,時間 t = τ において y (t) = 1 − e −1 ≃ 0.63 であるから,時定数とは,出力 y (t) が定常状態の約 0.63 倍となる時間となる.
7.2. 1 次遅れ要素のランプ応答
以下の伝達関数で表される 1 次遅れ要素のランプ応答を示す.ここで,τ は時定数とする.
入力及び出力の原関数を各々 x (t), y (t),これらの像関数を各々 X (s), Y (s) とすると,入力はランプ関数 x (t) = t, (t ≥ 0), X (s) = 1 / s2 であるから,出力 y (t) のラプラス変換 Y (s) は以下で与えられる.
1 / s2 の極は重極であるから,Y (s) は以下の部分分数に展開される.
留数定理より k1, k2, k3 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
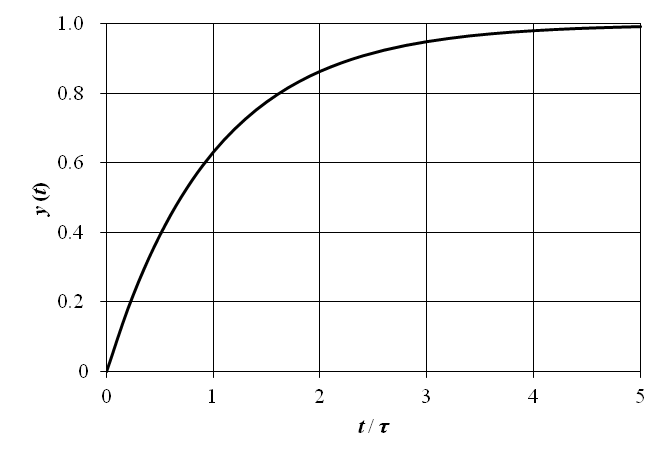
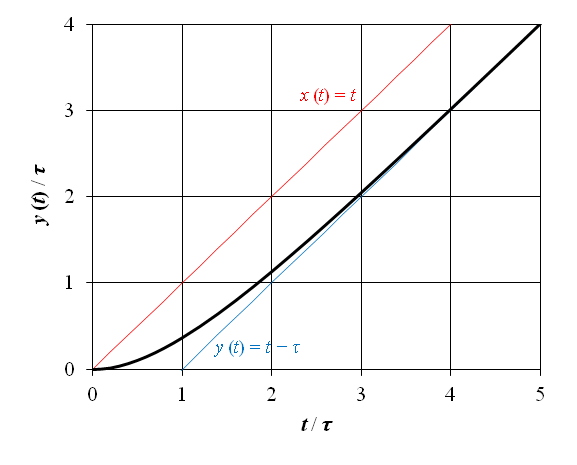
表5‑1 によるラプラス逆変換から,出力 y (t) は以下で与えられる.
上記の 1 次遅れ要素のランプ応答を図7‑2に示す.横軸の時間は t / τ,縦軸の出力は y (t) / τ として正規化されている.図の赤線は入力のランプ関数を示している.図から明らかな通り,出力 y (t) は t → ∞ で y (t) = t − τ に漸近する.よって,定常状態における入力 x (t) と出力 y (t) の間には,y (t) = x (t) − τ の差が生じるため x (t) = y (t + τ) の関係が成立する.
7.3. 1 次遅れ要素の正弦波応答
以下の伝達関数で表される 1 次遅れ要素の正弦波応答を示す.ここで,τ は時定数とする.
入力及び出力の原関数を各々 x (t), y (t),これらの像関数を各々 X (s), Y (s) とし,入力を振幅 1 初期位相 0 の正弦波 x (t) = sin (ωt), (t ≥ 0), X (s) = ω / (s2 + ω2) とすると,出力 y (t) のラプラス変換 Y (s) は以下で与えられる.
1 / (s2 + ω2) の極は複素数であるから,Y (s) は以下の部分分数に展開される.
留数定理より k1, k2, k3 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
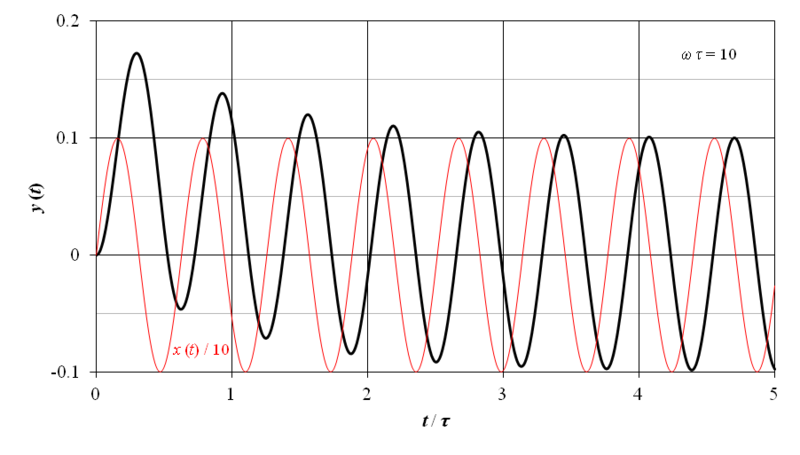
表5‑1 によるラプラス逆変換,及び式 (1‑14) に示した三角関数の合成定理から,出力 y (t) は以下で与えられる.
上記の右辺第 1 項は t → ∞ で 0 に収束する指数的減衰を,右辺第 2 項は正弦波振動を示している.入力は振幅 1 初期位相 0 の正弦波であるから,右辺第 2 項の正弦波振動の絶対値と偏角は,式 (6‑48) に示した 1 次遅れ要素の周波数伝達関数の絶対値と偏角と各々一致する.
ω τ = 10 における,上記の 1 次遅れ要素の正弦波応答を図7‑3に示す.横軸の時間は t / τ として正規化されている.また,図の赤線は正弦波入力を示しており,正弦波応答と視覚的に比較するために振幅を 1/10 に縮小して表示してある.
7.4. 2 次遅れ要素のインディシャル応答 (単位ステップ応答)
以下の伝達関数で表される 2 次遅れ要素のインディシャル応答を示す.ここで,ω0 は無減衰固有角周波数,ζ は減衰比とする.
入力及び出力の原関数を各々 x (t), y (t),これらの像関数を各々 X (s), Y (s) とすると,入力は単位ステップ関数 x (t) = u (t), X (s) = 1 / s であるから,出力 y (t) のラプラス変換 Y (s) は以下で与えられる.
ζ > 1 の場合
G (s) の極は実数で単極となるから,Y (s) は以下の部分分数に展開される.
留数定理より k1, k2, k3 は以下で与えられる (式の展開は省略).
よって Y (s) は以下の部分分数に展開される.
表5‑1 によるラプラス逆変換から,出力 y (t), (t ≥ 0) は以下で与えられる.
ζ = 1 の場合
G (s) の極は実数で重極となるから,Y (s) は以下の部分分数に展開される.
留数定理より k1, k2, k3 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
表5‑1 によるラプラス逆変換から,出力 y (t), (t ≥ 0) は以下で与えられる.
ζ < 1 の場合
G (s) の極は複素数となるから,Y (s) は以下の部分分数に展開される.
留数定理より k1 は以下で与えられる.
また,係数比較によりk2 = −1, k3 = −2 ζ ω0 となる.ここで式 (7‑29) の右辺第2項を式 (5‑22) の形式に展開する.
式 (5‑23) より σ, ω, K1, K2 は以下で与えられる.
よって Y (s) は以下の部分分数に展開される.
表5‑1 によるラプラス逆変換,及び式 (1‑14) に示した三角関数の合成定理から,出力 y (t), (t ≥ 0) は以下で与えられる.
応答のグラフ
以上の 2 次遅れ要素のインディシャル応答を図7‑4に示す.横軸の時間は ω0 t として正規化されている.図からも明らかな通り,ζ < 1 の場合は出力 y (t) は振動的となる.尚,振動解析では,ζ > 1 を過減衰,ζ = 1 を臨界減衰,0 < ζ < 1 を減衰振動,ζ = 0 を単振動と呼ぶ.
以下に続く.
6. 伝達関数と周波数応答
本章では,先ず伝達関数の定義,伝達関数の例,線形時不変システムの応答と伝達関数の関係を復習する.これらは教科書に十分な説明が記載されているため,本資料では数式の証明や導出等は省略し,留意すべき点を Note に示す.次に,6.4 において,周波数伝達関数はシステムの入出力の関係を記述する定数係数線形常微分方程式の定常解から定義される事を示し,初期条件が 0 とならず伝達関数が定義されないシステムにおいても,周波数伝達関数は定義される事を明らかにする.最後に 6.5 においてボード線図を復習する.
- 6.1. 伝達関数の定義
- 6.2. 伝達関数の例
- 6.3. 線形時不変システムの応答と伝達関数の関係
- 6.4. 周波数伝達関数の定義
- 6.5. ボード線図
- 余談: 本資料の周波数伝達関数の定義
- 本章の参考文献
6.1. 伝達関数の定義
入力の時間関数 x (t), (t ≥ 0) に対する出力の時間関数 y (t), (t ≥ 0) が,以下の定数係数線形常微分方程式で記述され,かつ初期条件が全て 0 となる線形時不変システムにおける,入力 x (t) と出力 y (t) のラプラス変換の比を,このシステムの伝達関数と言う.
初期条件を以下に示す.
上記の初期条件における,式 (6-1) のラプラス変換を以下に示す.
ここで,X (s), Y (s) は各々原関数 x (t), y (t) の像関数を表す.これを Y (s) について解くと以下の通りとなる.
よって,伝達関数 G (s) は以下で与えられる.
Note: 4.6 に述べた通り,定数係数線形常微分方程式の初期条件が全て 0 という事は,この方程式によって記述されるシステムが線形時不変システムである事を意味している.これは,式 (6-4) には零状態応答に対応する項のみが含まれ,零入力応答に対応する項が含まれないため,入力に対する重ね合わせの原理が成立する事からも明らかである.逆に言うと,定数係数線形常微分方程式の初期条件が 0 とならない場合,即ち零入力応答があるシステムには,伝達関数は定義されない.
6.2. 伝達関数の例
ローパスフィルタ (積分回路)
図6‑1 に示す,抵抗値が R [Ω] の抵抗,及びキャパシタンスが C [F] のコンデンサから成るローパスフィルタ (積分回路) の伝達関数を求める.ここで,入力電圧,出力電圧を各々 x (t), y (t) [V],回路に流れる電流を i (t) [A] とする.

式 (3‑16) より,キャパシタンスに流れる電流 i (t) [A] とこれに加わる出力電圧 y (t) [V] には以下の関係がある.
また,抵抗に流れる電流 i (t) [A] と入力電圧 x (t) [V] には以下の関係がある.
従って,上記の回路の入力電圧,出力電圧の関係は以下の定数係数線形常微分方程式で与えられる.
上記のラプラス変換を以下に示す.
伝達関数は初期条件 y (0) = 0 を前提としているから,上記のローパスフィルタの伝達関数 G (s) は以下となる.ここで τ = CR は時定数と呼ばれる.また,角周波数 ωc = 1 / τ はカットオフ周波数と呼ばれる.
上記の様に,分母の次数が 1 となる伝達関数を 1 次遅れの伝達関数と言う.
Note: 上記の回路の動作は,現実には入出力に接続される回路のインピーダンスの影響を受けるため,正確な動作が要求される場合は,演算増幅器 (オペアンプ) 等を使用するのが普通である.
ハイパスフィルタ (微分回路)
図6‑2に示す,抵抗値が R [Ω] の抵抗,及びキャパシタンスが C [F] のコンデンサから成るハイパスフィルタ (微分回路) の伝達関数を求める.ここで,入力電圧,出力電圧を各々 x (t), y (t) [V],回路に流れる電流を i (t) [A] とする.

式 (3‑16) より,キャパシタンスに流れる電流 i (t) [A] とこれに加わる入力電圧と出力電圧の差分 x (t) − y (t) [V] には以下の関係がある.
また,抵抗に流れる電流 i (t) [A] と出力電圧 y (t) [V] には以下の関係がある.
従って,上記の回路の入力電圧,出力電圧の関係は以下の方程式で与えられる.
上記のラプラス変換を以下に示す.
よって,上記のハイパスフィルタの伝達関数 G (s) は以下となる.ここで τ = CR は時定数と呼ばれる.また,角周波数 ωc = 1 / τ はカットオフ周波数と呼ばれる.
Note: 上記の回路の動作も,現実には入出力に接続される回路のインピーダンスの影響を受けるが,演算増幅器 (オペアンプ) 等を使用しても,増幅器の周波数特性による制限を受け,現実にはバンドパス特性のフィルタとなるため,正確な実現は非常に困難である.
バネマスダンパ系
図6‑3 に示す,ばね定数が k [N/m] のバネ,質量が m [Kg] のマス,減衰係数 (ダンピング係数) が c [Ns/m] のダンパ (ダッシュポット) から成るバネマスダンパ系において,入力を x (t) [N] の外力,出力を y (t) [m] の変位とした際の伝達関数を求める.
上記の運動方程式を以下に示す.
上記のラプラス変換を以下に示す.
伝達関数は初期条件 y' (0) = y (0) = 0 を前提としているから,上記のバネマスダンパ系の伝達関数 G (s) は以下で与えられる.
上記の様に,分母の次数が 2 となる伝達関数を 2 次遅れの伝達関数と言う.尚,振動解析ではこの式を下記の様に変形させる場合が多い.
ここで,ω0 は無減衰固有角周波数,ζ は減衰比と呼ばれる.ζ > 1 の場合は G (s) の極は実数で単極,ζ < 1 の場合は複素数となるから,伝達関数をこの様に変形する事によって,応答が指数的なのか振動的なのか,また固有振動数が容易に判る.
Note: 振動解析では,上記の様に外力によって引き起こされる振動を強制振動 (強制応答) と言う.
直列共振回路
図6‑4 に示す,抵抗値が R [Ω] の抵抗,インダクタンスが L [H] のコイル,及びキャパシタンスが C [F] のコンデンサから成る直列共振回路の伝達関数を求める.ここで,入力電圧,出力電圧を各々 x (t), y (t) [V],回路に流れる電流を i (t) [A] とする.

式 (3‑16) より,キャパシタンスに流れる電流 i (t) [A] とこれに加わる出力電圧 y (t) [V] には以下の関係がある.
また,式 (3‑9) より,抵抗,コイルに流れる電流 i (t) [A] と入力電圧 x (t) [V] には以下の関係がある.
従って,上記の回路の入力電圧,出力電圧の関係は以下の定数係数線形常微分方程式で与えられる.
上記のラプラス変換を以下に示す.
伝達関数は初期条件 y' (0) = y (0) = 0 を前提としているから,上記の直列共振回路の伝達関数 G (s) は以下で与えられる.
この伝達関数は,前記のバネマスダンパ系の伝達関数と本質的に同一となる.
むだ時間要素
システムの処理遅延等のむだ時間の伝達関数を求める.入力の時間関数を x (t),出力の時間関数を y (t),むだ時間を T とすると,これらの関係は以下の通りとなる.
表5-2 に示した時間軸上の平行移動の定理より,上記のラプラス変換は以下で与えられる.
従って,むだ時間要素の伝達関数 G (s) は以下で与えられる.
むだ時間要素の伝達関数は,システムに処理遅延がある場合だけでなく,サンプリングによるディジタル信号処理においても使用される.
フィードバック系
以下のブロックダイヤグラムで表される,伝達関数 G (s), H (s) から成るフィードバック系の伝達関数を求める.
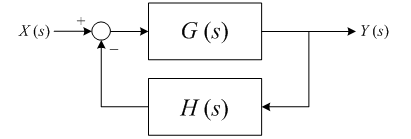
入力の時間関数を x (t),出力の時間関数を y (t) とすると,これらの像関数 X (s), Y (s) の関係は以下で与えられる.
従って,上記のブロックダイヤグラムで示されるフィードバック系の伝達関数 Y (s) / X (s) は以下で与えられる.
6.3. 線形時不変システムの応答と伝達関数の関係
インパルス応答
伝達関数 G (s) は入力の時間関数 x (t) と出力の時間関数 y (t) のラプラス変換の比であるから,これらの像関数 X (s), Y (s) の関係は以下の通りとなる.
ここで,入力を単位インパルス関数 δ (t) とした際の出力の時間関数をインパルス応答と言う.5.2 に述べた通り,単位インパルス関数のラプラス変換は 1 であるから,1 G (s) はインパルス応答のラプラス変換を示している.式 (6‑30) は以下の通り書き直せる.
上記の式と 5.2 に示した畳み込の公式より,システムのインパルス応答 g (t) が与えられれば,任意の入力の時間関数 x (t) に対する出力の時間関数 y (t) は以下の畳み込積分から得られる.
インディシャル応答 (単位ステップ応答)
残念ながら,単位インパルス関数は理論上,想像上の関数であるため,インパルス応答は物理的には実存しない.しかし,入力を単位ステップ関数 u (t) とした際の出力の時間関数であるインディシャル応答 (単位ステップ応答) からも類似の関係が得られる.単位ステップ関数のラプラス変換は 1 / s であるから,インディシャル応答のラプラス変換を A (s) とすると,これらの関係は以下の式で与えられる.
よって,式 (6-30) は以下の通り書き直せる.
上記の式と 5.2 に示した畳み込の公式,及び微分の公式より,システムのインディシャル応答 a (t) が与えられれば,任意の入力の時間関数 x (t) に対する出力の時間関数 y (t) は以下の式から得られる.
Note: 以上の関係は,あくまで伝達関数が定義される線形時不変システムにおいて成立する事に注意せよ.即ち,これらの関係は,初期条件が 0 とならならず伝達関数が定義されないシステムにおいては成立しない.
6.4. 周波数伝達関数の定義
入力の時間関数 x (t) に対する出力の時間関数 y (t) が,以下の定数係数線形常微分方程式で記述されるシステムに対して,入力 x (t) を複素正弦波 e jωtとし,出力 y (t) が入力と角周波数が等しい複素正弦波となる定常状態における入力 x (t) と出力 y (t) の比を,このシステムの周波数伝達関数 (周波数応答) と言う.
4.4 及び 4.5 に述べた通り,定常状態における出力 y (t) は,上記の定数係数線形常微分方程式における非同次方程式の特殊解 (定常解) yp (t) となる.よって,上記の式に,x (t) = e jωt を,また 4.4に述べた未定係数法に基づいて y (t) = A e j (ωt + φ) を代入すると,以下の通りとなる.
これを,入力 x (t) と出力 y (t) の比に整理すると下記の式が得られる.
上記の正弦波の時間関数の比における e jωt は約分され,時間関数が角周波数の関数に変換される.従って,周波数伝達関数 G (jω) は以下で与えられる.
ここで,以下に示す通り,周波数伝達関数 G (jω) の絶対値は,入出力される正弦波の振幅の比を,偏角は入出力される正弦波の位相差を示す.
Note: 以上の説明から明らかな通り,周波数伝達関数はシステムに入出力される正弦波の定常状態における振幅の比と位相差を示したものであり,定数係数線形常微分方程式の初期条件に依存しないため,初期条件が 0 とならず伝達関数が定義されないシステムにおいても,周波数伝達関数は定義できる事に注意せよ.更に,伝達関数と異なり入出力の時間関数の定義域に (t ≥ 0) の制約が無い事にも注意せよ.
6.1 に述べた上記と同じ定数係数線形常微分方程式で記述されるシステムにおいて,式 (6‑5) に示した伝達関数の s を jω に置き換えると,式 (6‑39) に示した周波数伝達関数となる.但し,この逆は必ずしも成り立たつとは限らない.初期条件が 0 とならない場合でも,周波数伝達関数は定義できるが,伝達関数は定義されない.
Note: 周波数伝達関数は定常状態においてシステムに入出力される正弦波の振幅の比と位相差を示したものである.一方,3 章に示した複素正弦波交流における誘導リアクタンス,容量リアクタンス,レジスタンス,及びこれらの直列回路,並列回路における複素合成インピーダンスは,何れも RCL による回路をシステムとすれば,複素正弦波交流の電流を入力,電圧を出力とした際の,定常状態における電圧と電流の振幅の比と位相差を示したものと解釈する事ができる.RCL による如何なる回路も,直列回路や並列回路の組み合わせであるから,RCL 回路における周波数伝達関数を求める際には,複素正弦波交流における誘導リアクタンス,容量リアクタンス,及びレジスタンスから計算する事ができ,伝達関数から求める必要は無い.
6.5. ボード線図
周波数伝達関数 G (jω) の絶対値及び偏角と周波数の関係を図示したものをボード線図と言う.前者はゲイン線図,後者は位相線図とも呼ばれる.周波数伝達関数の絶対値は入出力される正弦波の振幅の比を,偏角は入出力される正弦波の位相差を示すため,ボード線図はこれらと周波数の関係,即ちゲイン特性や位相特性等の周波数特性を図示したものとなる.
一般に,ボード線図は横軸に周波数 [Hz],若しくは角周波数 [rad/s] を対数目盛で取り,縦軸にG (jω) の絶対値 (Gain) をデシベル [dB] で,偏角 (Phase angle) を度 [deg] で表示する.デシベルとは,ある数値の常用対数を 20 倍したもので,20 dB の差は 10 倍を,6 dB の差は約 2 倍を意味する.|G (jω)| をデシベルで表すと以下の通りとなる.
積分要素のボード線図
上記の周波数伝達関数のボード線図を図6‑6に示す.図から明らかな通り,ゲイン特性は −20 [dB/decade] (周波数が 10 倍となると,ゲインは −20 [dB],即ち 1/10 倍) となる.また,位相特性は −90 [deg] (90度の位相遅れ) となる.上記から明らかな通り,積分要素のゲインは角周波数が 0 に近づくと無限大に発散するため,正確な積分要素を実現する事は出来ず,多くの場合,以下に述べるローパスフィルタ (積分回路) で代用する.

微分要素のボード線図
上記の周波数伝達関数のボード線図を図6‑7に示す.図から明らかな通り,ゲイン特性は 20 [dB/decade],位相特性は 90 [deg] (90度の位相進み) となる.上記から明らかな通り,微分要素は角周波数が高い領域でゲインが高くなるため,ノイズの影響を非常に受けやすい問題点がある.また,角周波数が無限大に近づくとゲインが無限大に発散するため,正確な微分要素を実現する事は出来ない.以下に述べるハイパスフィルタ (微分回路) で代用する場合もあるが,6.2 に述べた通りこれの正確な実現も困難である.
Note: そもそも,理論的には過去から現在までの信号の変化から,その現時点での微分を求める事は出来ないため,厳密な微分要素は理論上存在しない.次の瞬間に微分可能ではない変化をするかも知れない.5.4 において,制御理論では,ラプラス変換の分子の次数が分母の次数より高い場合は扱わないと述べたが,分子の次数の方が高い場合とは微分要素があるのと等価であり,その様な物は存在し得ないため扱う必要が無いのである.
1 次遅れ要素のボード線図 (ローパスフィルタ)
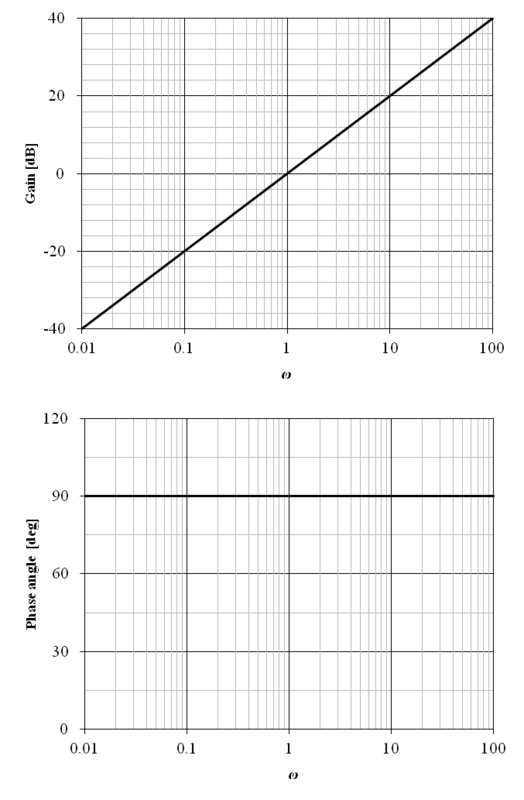
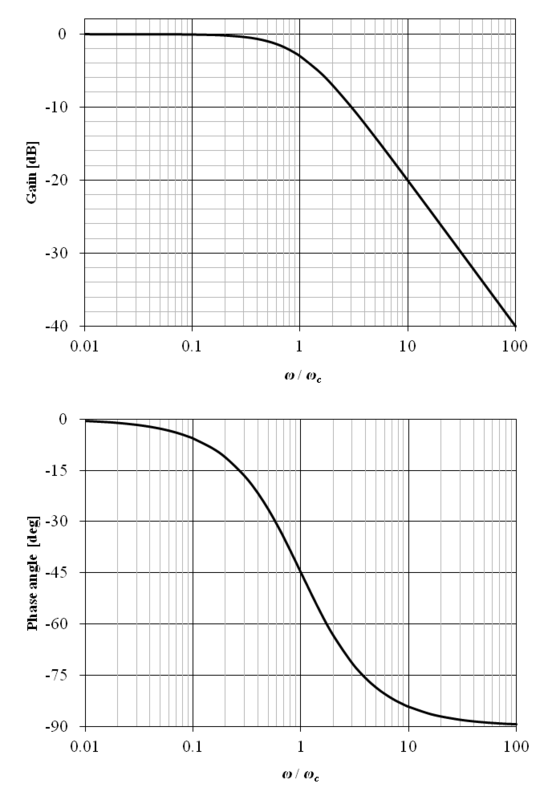
以下の伝達関数で表される 1 次遅れ要素 (ローパスフィルタ,積分回路) のボード線図を示す.ここで,τ は時定数,ωc = 1 / τ はカットオフ周波数とする.
従って,G (jω) の絶対値と偏角は以下の通りとなる.
上記の周波数伝達関数のボード線図を図6‑8に示す.横軸の角周波数は ω / ωc として正規化されている.
図から明らかな通り,ω / ωc ≪ 1 の場合のゲイン特性は 0 [dB] (1倍) となり,ω / ωc ≫ 1 の場合は −20 [dB/decade] となる.これは,20 [dB/decade] の減衰傾斜とも呼ばれる.ここで,図の中央のカットオフ周波数 ω = ωc におけるゲインは約 −3 [dB],即ち約 7/10 倍となる.これは,約 3 [dB] の減衰量とも呼ばれる.また,位相は −45 [deg] となる.
従って,この伝達関数で示される1 次遅れ要素はローパスフィルタとして動作する.また,ω / ωc ≫ 1 の周波数領域は積分要素の代用とする事ができる.
1 次遅れ要素のボード線図 (ハイパスフィルタ)
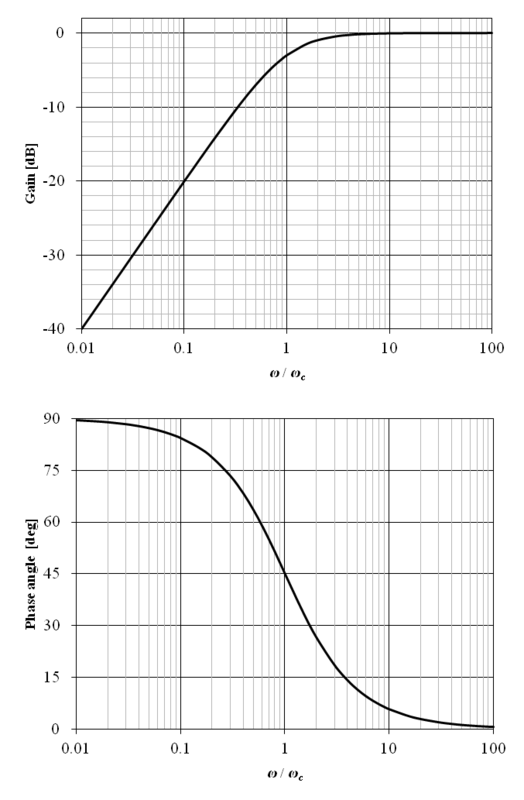
以下の伝達関数で表される 1 次遅れ要素 (ハイパスフィルタ,微分回路) のボード線図を示す.ここで,τ は時定数,ωc = 1 / τ はカットオフ周波数とする.
上記の周波数伝達関数のボード線図を図6‑9に示す.横軸の角周波数は ω / ωc として正規化されている.
図から明らかな通り,ハイパスフィルタとローパスフィルタのゲイン線図は,角周波数を逆数とした関係となる.ω / ωc ≪ 1 の場合のゲイン特性は 20 [dB/decade] となり,ω / ωc ≫ 1 の場合は 0 [dB] となる.ここで,図の中央のカットオフ周波数 ω = ωc におけるゲインは約 −3 [dB],位相は 45 [deg] となる.
従って,この伝達関数で示される1 次遅れ要素はハイパスフィルタとして動作する.また,ω / ωc ≪ 1 の周波数領域は微分要素の代用とする場合がある.但し,6.2 に述べた通り,現実にはハイパスフィルタの正確な実現は困難である.
2 次遅れ要素のボード線図
以下の伝達関数で表される 2 次遅れ要素のボード線図を示す.ここで,ω0 は無減衰固有角周波数,ζ は減衰比とする.
Note: 上記程度の複素関数の絶対値や偏角は,Excel や関数電卓で直接計算できるため,これらの式の展開は省略する.
上記の周波数伝達関数のボード線図を図6‑10に示す.横軸の角周波数は ω / ω0 として正規化されている.図から明らかな通り,ω / ω0 ≪ 1 の場合のゲイン特性は 0 [dB] となり,ω / ω0 ≫ 1 の場合は −40 [dB/decade] (周波数が 10 倍となると,ゲインは −40 [dB],即ち 1/100 倍) となる.これは 40 [dB/decade] の減衰傾斜とも呼ばれる.ここで,図の中央の無減衰固有角周波数 ω = ω0 近傍におけるゲインは減衰比 ζ に依存する.また,その際の位相は −90 [deg] となる.

むだ時間要素のボード線図
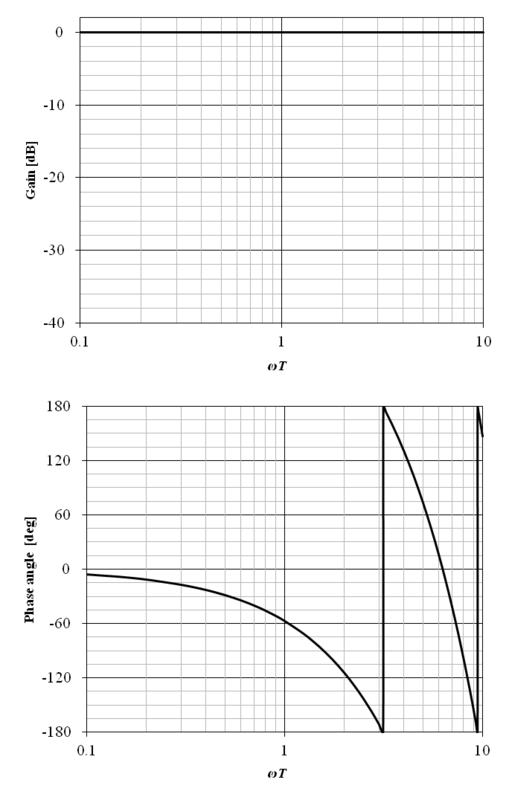
以下の伝達関数で表されるむだ時間要素のボード線図を示す.
上記の周波数伝達関数のボード線図を図6‑11に示す.横軸の角周波数は ωT として正規化されている.図から明らかな通り,むだ時間要素のゲイン特性は 0 [dB] となる.また,ω = π / T となる角周波数における位相は −180 [deg] となる.従って,むだ時間要素を含むフィードバック系のシステムにおいて,角周波数 ω = π / T におけるゲインが 0 [dB] を超える場合は,発振が生じる可能性がある.
以上が,むだ時間要素の教科書的説明である.ここで,システムの処理遅延等のむだ時間が伝達関数で記述できる事を直感的に説明する.上記のむだ時間要素の位相線図の横軸を直線軸とした図を以下に示す.
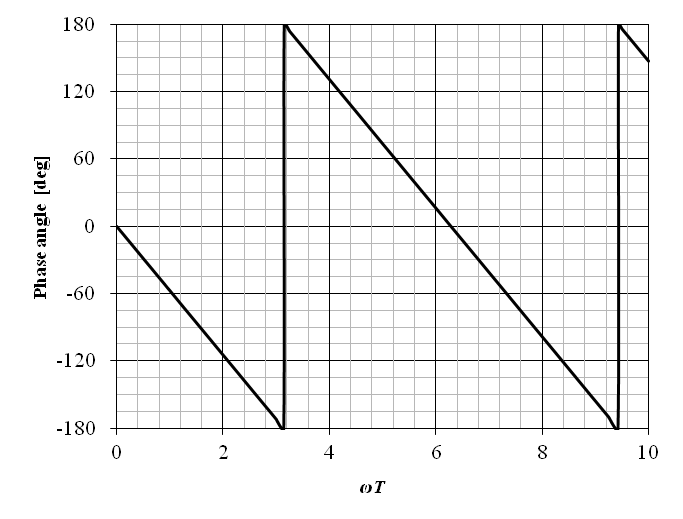
式 (6‑25) から明らかな通り,むだ時間要素とは,入力 x (t) から出力 y (t) への遅延時間が角周波数によらず一定となる要素の事である.従って,この遅延時間を周波数伝達関数における位相の遅れと考えると,むだ時間要素とは位相遅れが角周波数に比例する要素となる.むだ時間要素の周波数伝達関数は,この様な角周波数と位相遅れの関係を記述しているのである.但し,複素数の偏角の定義上,上の図に示す様に位相遅れが 180 [deg] を超えると 180 [deg] の位相進みとして表示される事に注意せよ.
Note: この考え方は,13.4 に述べる線形位相 FIR フィルタの基本となる.
余談: 本資料の周波数伝達関数の定義
6.4に述べた周波数伝達関数に関する解説は,殆どの制御工学の教科書の記述と大幅に異なるため,その理由を以下に説明する.
殆どの制御工学の教科書では,伝達関数において s = jω と変換した関数を周波数伝達関数として定義しているが,その理由が何も書かれておらず,即ち単に公式を天下り式に示しているだけで,何故そうなるのかが全く理解できない問題がある.但し,ごく一部の教科書には,伝達関数で記述された線形時不変システムの入力を正弦波とした際の,定常状態における入力と出力の比から周波数伝達関数を求める方法が示されているが,以下の観点からは説明が不足しているのである.
電気回路の周波数伝達関数を求める際に,制御工学の教科書通りに,入出力の関係を定数係数線形常微分方程式で記述し,ラプラス変換を行い,伝達関数を求めて,s = jω と変換するやり方は,正直の上に馬鹿が付く解法である.本資料の 3 章が理解できていれば,電気回路における周波数伝達関数は,回路の複素合成インピーダンスから直ちに求める事ができる.
周波数伝達関数の導出に,定数係数線形常微分方程式の記述,ラプラス変換と伝達関数の算出,伝達関数への正弦波の入力と定常状態における出力の算出といった教科書通りの手順が必要であるとすれば,何故,本資料の 3 章に示した複素合成インピーダンスに基づく遥かに簡単な解法によって,これと等価な結果が導けるのか,説明が必要なのである.即ち,制御工学の教科書の周波数伝達関数の説明では,電気工学における複素インピーダンスによる解法との関係が全く不明なのである.或いは,これらは厳密には制約条件や適用範囲が異なる問題に対する異なる解法なのか,という疑問が生じる.
本資料では電気工学と整合性の取れた周波数伝達関数の解法を示している.4.5 章に述べた通り,3 章に示した複素合成インピーダンスは,定数係数線形常微分方程式によって記述されたシステムにおいて,入力を複素正弦波 e jωtとし,出力を非同次方程式の特殊解 (定常解) yp (t) から求める方法で導出している.このため,本資料でもこの方法によって,周波数伝達関数を求めている.ごく一部の制御工学の教科書に示された伝達関数から周波数伝達関数を求める解法には過渡現象が含まれてしまうため,本資料の様に定常解を直接求めた方が容易に理解できるし,初期条件に依存しないため,伝達関数が定義されない場合にも対応できる.
本章の参考文献
明石一, "制御工学 増訂版," 大学講座 機械工学 12, 共立出版, 1979.
5. ラプラス変換と定数係数線形常微分方程式
本章では,ラプラス変換の定義,公式と定理,ラプラス変換による定数係数線形常微分方程式の解法を復習する.これらは教科書に十分な説明が記載されているため,本資料では数式の証明や導出等は省略し,留意すべき点を Note に示す.
- 5.1. ラプラス変換の定義
- 5.2. ラプラス変換の公式と定理
- 5.3. ラプラス変換による定数係数線形常微分方程式の解法
- 5.4. 逆変換における部分分数への分解方法
- 余談: 何故ラプラス変換で定数係数線形常微分方程式が解けるのか
- 本章の参考文献
5.1. ラプラス変換の定義
t ≥ 0 で定義された関数 f (t) のラプラス変換 F (s) を以下に示す.
ここで s は複素数で s = σ + jω と表す事が多い.また,f (t) を原関数,F (s) を像関数,F (s) が収束する s の範囲を収束域と言う.原関数 f (t) と像関数 F (s) の関係を以下の様に表示する場合もある.
同様に,原関数 f (t) は像関数 F (s) のラプラス逆変換とも呼ばれ,以下の様に表示される.
ラプラス逆変換の公式を以下に示す.
Note:原関数 f (t) の定義域は t ≥ 0 となる事に注意せよ.式 (5‑1) から明らかな通り,原関数 f (t) の t < 0 の部分は像関数 F (s) に影響を与えない.このため,原関数 f (t) の t < 0 に意味を持たせてはならない.同様に,逆変換の結果得られる原関数 f (t) の t < 0 の部分には意味は無い.即ち,原関数 f (t) の t < 0 は不定となる.これは線形時不変システムを分析する際には殆ど問題とはならないが,定数係数線形常微分方程式をラプラス変換によって解く場合,4 章に示した方法と比較して若干の制約となる事に留意せよ.
尚,ラプラス変換は,定数係数線形常微分方程式の解法や線形時不変システムの解析に用いられるが,フーリエ解析の様に観測した信号をラプラス変換する事や,任意の原関数をラプラス変換する必要が生じる事は稀である.このため,上記のラプラス変換,逆変換の公式を実際に解く必要は殆ど無く,多くの場合変換,逆変換には以下のラプラス変換の公式や定理が用いられる.
5.2. ラプラス変換の公式と定理
ラプラス変換の主要な公式を以下に示す.
| 項番 | 原関数 |
像関数 |
収束域 |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 | |||
| 11 |
項番 1 の原関数は単位インパルス関数やデルタ関数と呼ばれる超関数である.これは,虚数と同様に物理的な事象を記述したものではなく,理論上,想像上の関数であり,下記で定義される.
ここで,f (t) = 1 とすると,単位インパルス関数の面積は 1 となる事が判る.
一方,式 (5‑5) を満たすには,単位インパルス関数は t ≠ 0 において δ (t) = 0 となる.従って,t = 0 において形式的に δ (0) = ∞ と見做される.尚,式 (5‑5), (5‑6) は積分範囲を [−∞,∞] としているが,以下に示す様に積分範囲に 0 が含まれていれば,これらの式は成り立つとされている.
項番 2 の原関数は単位ステップ関数と呼ばれる.原関数の定義域は t ≥ 0 であるから,これを項番 3 の様に表す場合もある.単位インパルス関数は,以下の通り単位ステップ関数の微分であると考えても良い.
項番 4 はランプ関数や定速度関数と呼ばれ,サーボ系の定常偏差の評価に良く用いられる.項番 10, 11 は各々項番 8, 9 を s 領域で平行移動したものである.
Note: ラプラス変換の原関数の定義域が t ≥ 0 である事から,これを明示するために原関数を sin (ωt) u (t) の様にステップ関数との積で表示する流儀もある.
最後に,ラプラス変換の主要な定理を以下に示す.
| 線 形 性 | |
| 微 分 | |
| 積 分 | |
| 畳み込み | |
| 時間軸上の平行移動 | |
| s 領域の平行移動 | |
| 最終値定理 | |
| 初期値定理 |
5.3. ラプラス変換による定数係数線形常微分方程式の解法
ラプラス変換による下記の 2 階定数係数線形常微分方程式の初期値問題における特殊解の解法を示す.高階の場合も解法は原理的に同じである.
上記の両辺のラプラス変換を以下に示す.
ここで,X (s), Y (s) は各々原関数 x (t), y (t) の像関数を表す.上記を Y (s) について解き,初期条件を代入すると以下の通りとなる.
上記は原関数 y (t) のラプラス変換を与えるから,これを下記の様に逆変換する事によって y (t) の初期値問題における特殊解が得られる.
逆変換は,式 (5‑11) の各項を部分分数に分解して,ラプラス変換の公式に当てはめる方法が簡易である.この方法は 5.4 に述べる.
Note: 式 (5‑11) の分母 a2 s 2 + a1 s + a0 を 0 とした方程式は,式 (5‑9) を x (t) = 0 とした同次方程式における特性方程式と等しい事に注意せよ.
Note: 式 (5‑12) の右辺第 1 項は初期条件に依存し,入力に依存しないため零入力応答,第 2 項は入力に依存し,初期条件に依存しないため零状態応答と呼ばれる.尚,零状態応答には過渡現象が含まれており,零入力応答や零状態応答は,同次方程式の一般解 (過渡解) yc (t) や非同次方程式の特殊解 (定常解) yp (t) と 1 対 1 の対応関係は無い.
5.4. 逆変換における部分分数への分解方法
式 (5-11) の各項を部分分数に分解する具体的な方法を説明する.部分分数分解は高校数学で学習しているし,直感で解いても差し支えないが,ここでは汎用性の高い留数定理 (ヘビサイドの展開定理) に基づいた方法を示す.説明を簡単にするために,下記に示した,分母の次数が 2 次,分子の次数が 1 次となる像関数の部分分数への分解方法を示す.
ここで,上記の式の分母を 0 とした以下の方程式を,特性方程式と呼ぶものとする.
Note: 分子と分母の次数が共に 2 次となる場合は,下記の様に定数項を繰り出して,分子の次数を 2 次以下とする.この定数項はインパルス関数に逆変換される.従って,この様な分子と分母の次数が等しい像関数の逆変換は,インパルス応答の様な論理上,想像上の応答を求める場合には考えられるが,現実的な過渡現象を求める場合には通常はあり得ない.
尚,制御理論では,分子の次数が分母の次数より高い場合は扱わないため,その様な場合は考えなくてよい.
Y (s) の極が実数で単極の場合
これは,特性方程式の s が異なる実数解となる場合であるから,これらを各々 α, β とすると像関数は以下の様に部分分数に分解できる.
ここで,k1, k2 は以下の様に留数定理 (ヘビサイドの展開定理) から求められる.
以上とラプラス変換表より,原関数 y (t) の特殊解は以下の通りとなる.
Y (s) の極が実数で重極の場合
これは,特性方程式の s が重解となる場合であるから,これを α とすると像関数は以下の様に部分分数に分解できる.
ここで,k1, k2 は以下の様に留数定理から求められる.
以上とラプラス変換表より,原関数 y (t) の特殊解は以下の通りとなる.
Y (s) の極が複素数の場合
これは,特性方程式の s が共役複素数となる場合であり,上に示した極が実数で単極の場合と同じ方法で解けるが,計算が煩雑となる.この場合は,以下の様に係数比較によってラプラス変換の公式に変換した方が簡単である.ここで,特性方程式における s の共役複素数の解を σ ± jω とする.
上記の係数を比較すると下記が得られる.
以上とラプラス変換表より,原関数 y (t) の特殊解は以下の通りとなる.
上記に式 (1-14) に示した三角関数の合成定理を適用しても良い.
分母の次数が 3 次以上の場合
像関数の分母の次数が 3次以上の場合の分解方法は 2次の場合と原理的に同じとなる.何故なら,n 次の多項式には複素数を含む n 個の根があるため,像関数の極が実数の場合は分母の次数が 1 次の部分分数,複素数の場合は分母の次数が 2 次の部分分数に分解できるからである.
分母の次数が 3 次以上となる場合は,以下の様に Y (s) の極が複素数と実数となる際の部分分数への分解方法が必要となる.
ここで,右辺 1 項の特性方程式における s の共役複素数の解を σ ± jω とすると,k1, k2 は以下の様に係数比較によって求める事ができる.
また,分母の次数が 3 次以上となる場合は重極の扱いも必要となる.例えば n 重極の場合,原関数は以下の様に部分分数に分解できる.
ここで,kr は以下の留数定理から求められる.
また,複素数の重極の場合は,原関数を以下の様に部分分数に分解しても良い.
余談: 何故ラプラス変換で定数係数線形常微分方程式が解けるのか
本資料を作成するにあたって,この問題を考えたが,気の利いた説明を見出せなかった.そもそも,微分方程式が何故解けるのか,との問いを考えても,教科書に載っている微分方程式は解法が判明しているものに限られ,大抵の高階非線形の微分方程式は解析的には解けず,数値計算によって数値解を求めるしか無いのである.
4.3,4.4 に述べた定数係数線形常微分方程式の解法は,これの一般解が指数関数的減衰 (或いは発散) と正弦波振動の組み合わせにしかならない事を利用している.ラプラス変換による解法もこれと根本的に異なる方法では無く,類似の点が多く見られ,解法をさらに洗練しパターン化定型化している様に思える.
すると,結局ラプラス変換の定義である式 (5‑1) による積分変換が何を意味しているのか,という事になるが,適切な説明に思い至らなかった.多くの教科書や資料に書かれている通り,ラプラス変換に物理的なイメージを見出す事は難しく,指数関数や対数関数と同様の計算量を削減する数学的手法と見做すことが妥当であろう.
一部の資料においてラプラス変換の定義式を s = jω としてフーリエ変換と類似の式として考察している場合が見受けられるが,それでは定常解が解ける事の直感的な説明にしかならないであろう.ラプラス変換の積分変換における複素指数関数の指数は s = σ + jω であるため,これは以下の図の様に複素平面上で指数関数的減衰と正弦波振動を同時に表す事を暗喩しており,この様な関数における何らかの直交性を利用した変換を行っているのではないかと想像する.

図5‑1: 複素平面上における exp (σ + jω) t (t ≥ 0, σ < 0).
上記を σ > 0 とし更に時間軸を加えて 3 次元表示にすると EXILE のグルグルとなるのである.
本章の参考文献
明石一, "制御工学 増訂版," 大学講座 機械工学 12, 共立出版, 1979.
4. 線形時不変システムと定数係数線形常微分方程式
本章では,先ず 4.1 において線形時不変システムの定義とその意味を述べる.次に 4.2 において線形時不変システムの入出力の関係の記述に用いられる定数係数線形常微分方程式の概要を示す.そして 4.3,4.4 において定数係数線形常微分方程式の一般解の解法を復習し,4.5 において線形時不変システムの記述の観点からこの解法の意味を述べる.最後に 4.6 において,定数係数線形常微分方程式によって記述されるシステムは,初期条件がすべて 0 であれば線形時不変システムの条件を満たし,さもなければ,初期条件による出力への影響が無視できる定常状態において,線形時不変システムと見做せる事を示す.
- 4.1. 線形時不変システムの定義
- 4.2. 定数係数線形常微分方程式
- 4.3. 定数係数線形常微分方程式の解法 (同次方程式)
- 4.4. 定数係数線形常微分方程式の解法 (非同次方程式)
- 4.5. 定数係数線形常微分方程式の解法の意味
- 4.6. 線形時不変システムと定数係数線形常微分方程式の関係
4.1. 線形時不変システムの定義
入力の時間関数 x (t) に対する出力の時間関数が y (t) となるシステム G において,これら時間関数の関係を式 (4‑1) の形式で表示するものとする.

ここで,システム G における入力 x1 (t), x2 (t),出力 y1 (t), y2 (t) が以下の関係を満たす場合,システム G を線形システムと言う.ここで a, b は定数である.
上記の定義は,入力を a 倍したら出力も a 倍される直線性を有し,かつ複数の入力が加えられた場合の出力は,個々の入力が加えられた際の出力の和となる,重ね合わせの原理が成立するシステムを規定している.
また,システム G における入力 x (t),出力 y (t) が以下の関係を満たす場合,システム G を時不変システムと言う.ここで τ は定数である.
上記の定義は,入力と出力の関係が,時間 t の原点の取り方に依存しないシステムを規定している.
Note: 線形時不変システムに該当しないシステムの例として,信号間で乗算が行われるシステムや,非線形性を利用しているシステムが挙げられる.具体的な例としては,変調回路 (振幅変調,周波数変調,位相変調を問わず),復調回路,周波数変換回路,周波数逓倍回路,整流回路,対数増幅回路等が挙げられる.
4.2. 定数係数線形常微分方程式
線形時不変システムの入力の時間関数 x (t) と出力の時間関数 y (t) の関係は,下記の常微分方程式で記述される.下記の常微分方程式は y (t) を未知関数とし,これとその導関数の一次式から成るため,線形常微分方程式であり,かつ an, ..., a0 は定数であるため,定数係数線形常微分方程式と呼ばれる.
以降,上記の常微分方程式を下記の様に記す.
これは一見非常に難解な式であるため,直感的な理解のために,上記の式の意味を大雑把に説明する.式 (4‑5) の出力 y (t) を正弦波と考える.2.4 に述べた通り,正弦波を時間微分しても角周波数は変化しない.何回微分しても角周波数は同じである.また,式 (4‑5) の左辺はこれらの一次結合を表している.1.3 及び 2.5 に述べた通り,角周波数が等しい正弦波を合成すると,これらと角周波数が等しい正弦波となる.これは,正弦波が変位によって表示される場合でも,正弦波の複素数表示の場合でも同様に成立する.
この様な予備知識を持って再度式 (4‑5) を見ると,この式は,入力 x (t) を正弦波とした場合,出力 y (t) がこれと角周波数が等しい正弦波となるシステムを示している事が容易に理解できる.振幅と初期位相は変化するかも知れないが角周波数は変化しない.式 (4‑5) はこの様な単純な関係を一般的な形式で記述しているだけなのである.
残念ながら,以上の説明に誤りは無いのだが,定数係数線形常微分方程式には無数の解があり,上記はその特殊解の一つについて述べているだけで,網羅性を欠いている.解によっては,定数係数線形常微分方程式で記述されたシステムが,線形時不変システムの条件を満たさない場合もある.そこで,以下定数係数線形常微分方程式の解法を復習し,線形時不変システムとの関係をより正確に示す.
4.3. 定数係数線形常微分方程式の解法 (同次方程式)
Note: 定数係数線形常微分方程式の初期値問題における特殊解を求める方法としては,以下の教科書的解法より,5 章に示すラプラス変換による解法の方の手順が定型化しているため習熟が容易である (尚,計算の手間はどちらでも大差ない).このため,以下の解法に習熟する必要は無いが,定常状態の解を求める場合は以下の方が容易である事,またラプラス変換において,以下の一般解を求める過程で使用される特性方程式に関する知識が必要となるため,基本的な考え方を理解しておく必要はある.
説明を簡単にするため,下記の 2 階定数係数線形常微分方程式の一般解の解法を示す.高階の場合も解法は原理的に同じである.
上記の常微分方程式の解法のステップは以下の通りとなる.
- 式 (4‑6) の入力を x (t) = 0 とした同次 (斉次) 方程式を解き,これの一般解を yc (t) とする.
- 非同次方程式である式 (4‑6) の特殊解の一つを求め,これを yp (t) とする.
- 重ね合わせの原理により,式 (4‑6) の一般解を y (t) = yc (t) + yp (t) とする.
先ず,最初のステップとして,式 (4‑6) の入力を x (t) = 0 とした,下記の同次方程式の一般解の解法を示す.
上記の同次方程式の特殊解は yc (t) = e st の形となる事が既知であるため,これを上記に代入する.
よって,s を求めるには下記の方程式を解けば良い.下記は式 (4‑7) の特性方程式と呼ばれる.
特性方程式の解が異なる実数の場合
特性方程式における s の実数解を各々 α, β とすると,同次方程式 (4‑7) の一般解は下記の通りとなる.ここで C1, C2 は任意定数である.
特性方程式の解が実数の重解の場合
特性方程式における s の重解を α とすると,同次方程式 (4‑7) の一般解は下記の通りとなる.ここで C1, C2 は任意定数である.
特性方程式の解が共役複素数の場合
特性方程式における s の共役複素数の解を σ ± jω とすると,オイラーの公式より,同次方程式 (4‑7) の一般解は下記の通りとなる.ここで C1, C2 は任意定数である.
上記に式 (1 14) に示した三角関数の合成定理を適用しても良い.
高階の定数係数線形常微分方程式の場合
高階の場合は重解の扱いが必要となる.例えば s が実数の 4 重解の場合は,一般解は下記の形式となる.
同様に,例えば s が複素数の 2 重解の場合は,一般解は下記の形式となる.
他にも解がある場合は,それらの一次結合が一般解となる.
4.4. 定数係数線形常微分方程式の解法 (非同次方程式)
次のステップとして,非同次方程式である式 (4-6) の特殊解の一つを求める方法を示す.これには定数変化法と未定係数法という異なる方法がある.前者は正攻法であるが極めて煩雑であるため,本資料では未定係数法について述べる.
未定係数法とは,式 (4‑6) の入力 x (t) の形に応じて,非同次方程式の特殊解 yp (t) の形を推定して,式 (4‑6) に代入して yp (t) を求める方法である.
x (t) が多項式の場合
例えば,x (t) が 2 次の多項式 x (t) = t 2 + 2 t + 1 の場合,多項式を微分しても多項式となるから,非同次方程式の特殊解 yp (t) を 2 次の多項式 yp (t) = A t 2 + B t + C と推定し式 (4‑6) に代入して,これらの係数を求める.
x (t) が指数関数の場合
例えば,x (t) が x (t) = e at の場合,指数関数を微分しても指数部が等しい指数関数となるから,非同次方程式の特殊解 yp (t) を指数関数 yp (t) = C e atと推定し式 (4‑6) に代入して,この係数を求める.
x (t) が正弦関数,余弦関数の場合
例えば,x (t) が x (t) = sin (ωt) や x (t) = cos (ωt) の場合,正弦関数や余弦関数を微分しても角度が同じ余弦関数や正弦関数となるから,非同次方程式の特殊解 yp (t) を yp (t) = A sin (ωt) + B cos (ωt) と推定し式 (4‑6) に代入して,これらの係数を求める.
x (t) が上記の一次結合となる場合
例えば,x (t) が x (t) = e at + sin (ωt) の場合,重ね合わせの原理により,非同次方程式の特殊解を yp (t) = yp1 (t) + yp2 (t) とし,上記と同様に yp1 (t) = C e at,yp2 (t) = A sin (ωt) + B cos (ωt) と推定し式 (4‑6) に代入して各々の係数を求める.
尚,上記で推定した非同次方程式の特殊解 yp (t) の係数を除く形式が,同次方程式の一般解 yc (t) の各項の任意定数を除く形式と同一となってしまう場合は,推定した特殊解を t 倍する.
最後のステップとして,非同次方程式の特殊解 yp (t) が求められ場合は,式 (4‑6) の非同次方程式の一般解は y (t) = yc (t) + yp (t) となる.
4.5. 定数係数線形常微分方程式の解法の意味
以上の定数係数線形常微分方程式の解法は,非常に煩雑であり,かつ果たしてこれが本当に数学なのかと疑念を抱きたくなる内容であるため,線形時不変システムの記述という観点から上記の解法の意味を述べる.
同次方程式の一般解 yc (t)
特性方程式の解が実数解,重解,共役複素数何れの場合でも,α < 0, β < 0, σ < 0 であれば,これらの式の形式から明らかな通り,同次方程式の一般解 yc (t) は t → ∞ で 0 に収束する出力を表している.このため,制御工学や電気工学では,同次方程式の一般解を yc (t) を過渡解と言う場合がある.
Note: 式 (4‑11) や (4‑13) に現れる t n e −st, (s > 0) は一見 t → ∞ で不定となる様に思えるが,下記の通りロピタルの定理で分子分母を n 回微分すれば 0 に収束する.
Note: α < 0, β < 0, σ < 0 以外の場合は t → ∞ で出力が発散,若しくは 0 に収束せず実用的では無いため,制御工学や電気工学ではこの様な場合は一般には扱わない.
非同次方程式の特殊解 yp (t)
未定係数法による非同次方程式の特殊解 yp (t) の解法は,線形時不変システムの観点からは,入力 x (t) を与えて,これに対する出力 yp (t) を求める方法と見做せる.ここで,出力 yp (t) は特殊解であり任意定数を含まないため,微分方程式の初期条件に依存しない.従って,非同次方程式の特殊解 yp (t) は入力のみに依存し,定常状態における出力を表すため,制御工学や電気工学ではこれを定常解と言う場合がある.
4.2 に述べた定数係数線形常微分方程式の大雑把な説明は,上記の非同次方程式の特殊解 yp (t) に関するものである.尚,入力 x (t) は正弦波に限らない.直流を入力する場合は,入力 x (t) を定数とすれば良い.定数は多項式の一つである.
Note: 3章に示した定常状態における交流回路は,コイルやコンデンサに加わる電圧や流れる電流の関係を入力や出力と見做せば,定数係数線形常微分方程式で記述されたシステムとなる.3.2や 3.3の複素正弦波交流における式の展開,例えば式 (3‑9) の微分方程式に対して,式 (3‑11) や (3‑14) の様に正弦波の時間関数を代入している箇所,は未定係数法と類似の方法で,非同次方程式の特殊解 yp (t),即ち定常解を求めていると解釈できる.
非同次方程式の一般解 y (t)
前に述べた通り,非同次方程式の一般解 y (t) は,同次方程式の一般解 (過渡解) yc (t) と非同次方程式の特殊解 (定常解) yp (t) の和となる.ここで,非同次方程式の一般解 y (t) を初期条件の下で解いた初期値問題の特殊解は,定数係数線形常微分方程式で記述されたシステムの過渡現象を示す.
Note: 同次方程式の一般解 (過渡解) yc (t) が過渡現象を示す訳では無い事に注意せよ.過渡解という用語は誤解を招きやすい.
Note: システムの過渡現象を求めるために,同次方程式の一般解 (過渡解) yc (t) に対する初期値問題を解いても誤りとなる.それは x (t) = 0,即ちシステムに入力が無い際の出力 y (t) を求めるという,別の問題を解いている事になる.
以上,定数係数線形常微分方程式の解法に対して,線形時不変システムの記述という観点からの意味を明らかにしたが,この様な観点からこの解法を見ると,これが果たして本当に数学なのかという疑念は益々深まるのである.
4.6. 線形時不変システムと定数係数線形常微分方程式の関係
定数係数線形常微分方程式の解法は,これの同次方程式や非同次方程式の特殊解に対して,微分演算の線形性や重ね合わせの原理が成り立つ事を利用して一般解を求めている.しかし,これだけでは定数係数線形常微分方程式で記述されたシステムが4.1に示した線形システムの条件を満たしているとは言えない.何故ならば,実際のシステムの出力 y (t) は初期値問題における特殊解となり,初期条件によっては,入力 x (t) = 0 の際に出力 y (t) = 0 とならない場合,即ち入力が無くても出力が現れる場合があり,この様なシステムでは,重ね合わせの原理は当然成立しないからである.
Note: 線形システムの条件を満たさない具体的な例として,初期状態においてシステムを構成する回路中のコンデンサに電荷が蓄えられており,入力と無関係にコンデンサの放電による出力が現れる場合が挙げられる.
Note: 定数係数線形常微分方程式の係数は定数であり時間に依存しないため,時不変システムの条件は満足される.
このため,定数係数線形常微分方程式で記述されたシステムが,入力 x (t) = 0 において,出力 y (t) = 0 となれば,線形時不変システムの条件を満たす.4.3 に示した同次方程式の一般解 (過渡解) yc (t) を初期条件の下で解いた初期値問題の特殊解は,入力 x (t) = 0 における出力を示す.このため,この同次方程式の特殊解が yc (t) = 0 となれば線形時不変システムの条件を満たす事になる.式 (4‑7) を以下に再度示す.
上記の同次方程式の特殊解が yc (t) = 0 となる場合は以下も成立する.
従って,(4‑16) の同次方程式の初期値問題を下記の初期条件で解いた場合,特殊解は yc (t) = 0 となる.
即ち,t = 0 における初期条件が全て 0 となる定数係数線形常微分方程式によって記述されたシステムは線形時不変システムの条件を満たす.また,初期条件が 0 とならず,同次方程式の特殊解が yc (t) = 0 とならない場合であっても,4.5 に述べた通りこれは実用的な条件下では t → ∞ で 0 に収束するため,この影響が無視できる定常状態において,線形時不変システムの条件を満たすと見做せる.
Note: t = 0 における初期条件が全て 0 の場合,同次方程式の特殊解が yc (t) = 0 となる事は,システムからの出力が非同次方程式の特殊解 (定常解) yp (t) による出力のみとなり,過渡現象が無くなる事を意味している訳では無い.この場合のシステムからの出力は非同次方程式の一般解 y (t) において,初期条件を全て 0 とした初期値問題の特殊解となる (y (t) の一般解におけるyc (t) は一般解であり,特殊解では無い).