13. FIR フィルタの概要

本章では，13.1 において FIR (Finite Impulse Response) フィルタ (有限インパルス応答フィルタ，非巡回型フィルタ) の基本を，13.2 において基本的な FIR フィルタの例を，13.3 において窓関数による FIR フィルタの例を述べる．次に，13.4 において，位相歪が生じない線形位相フィルタの直感的な原理を述べ，13.5 において線形位相フィルタのインパルス応答の例を示す．そして，13.6 においてこれに基づいた線形位相 FIR フィルタの例を，13.7 において窓関数による線形位相 FIR フィルタの例を示す．これらは教科書に十分な説明が記載されているため，本資料は留意すべき点を Note に示す．

13.1. FIR フィルタの基本

システム伝達関数 H (z) が以下の式で与えられるディジタルフィルタの構造を示す．ここで，h [n], (n ≥ 0) はディジタルフィルタのインパルス応答を，X (z), Y (z) は各々ディジタルフィルタの入出力となる離散時間信号 x [n], y [n], (n ≥ 0) の Z 変換を示す．

$$\begin{array}{}\text{(13-1)}& H\left(z\right)=\frac{Y\left(z\right)}{X\left(z\right)}=\sum _{n=0}^{N-1}h\left[n\right]{\mathrm{<mspace\; width="0.1em"></mspace>}z}^{-n}\end{array}$$

上記のディジタルフィルタに入出力される離散時間信号 x [n], y [n] の関係は，以下の畳み込みで記述される．

$$\begin{array}{}\text{(13-2)}& y\left[n\right]=\sum _{k=0}^{N-1}h\left[k\right]\mathrm{<mspace\; width="0.1em"></mspace>}x\left[n-k\right]\end{array}$$

FIRフィルタとは，上記の畳み込みによる離散時間信号 x [n], y [n] の関係をフィルタの実現アルゴリズムと見做したものであり，出力の離散時間信号 y [n] を現在及び過去 N − 1 回の入力 x [n], ..., x [n − (N − 1)] から求める．

FIR フィルタの基本構造を図13‑1に示す．図において，四角は入力信号に 1 サンプリング周期の遅延を加えて出力するレジスタ，三角は定数係数の乗算器，丸は加算器を示し，上記の畳み込みの関係を式の通りに計算する．レジスタの初期値は全て 0 となる．ここで，FIR フィルタの次数 N − 1 は，レジスタ数となる．

図13-1: FIR フィルタの基本構造．

上記の基本構造から明らかな通り，FIR フィルタの設計にはインパルス応答を求める必要がある．フィルタが満たすべき周波数伝達関数を H_d (e ^jωT) とすると，式 (12‑11) に示した離散時間フーリエ変換 (DTFT) の逆変換からインパルス応答を求める事が出来る．但し，式 (12‑11) の積分を求める事が容易では無い場合は，周波数伝達関数をサンプリングして，式 (12‑4) に示した離散フーリエ変換 (DFT) の逆変換からインパルス応答の近似を求めても良い．勿論，フィルタが満たすべきシステム伝達関数の逆 Z 変換からインパルス応答を求めても良い．

多くの場合，フィルタが満たすべき周波数伝達関数 H_d (e ^jωT) に対応したインパルス応答 h [n] は無限に続くため，H_d (e ^jωT) と h [n] の関係は以下で記述される．

$$\begin{array}{}\text{(13-3)}& H_d\left(e^{j\omega T}\right)=\sum _{n=0}^{\mathrm{\infty }}h\left[n\right]e^{-jn\omega T}\end{array}$$

ディジタル信号処理では，入出の離散時間信号 x [n] が出力の離散時間信号 y [m], (n > m) に影響を及ぼす事はあり得ないため，インパルス応答は必ず h [n] = 0, (n < 0) となる．また，ディジタル信号処理では，初期条件を 0 とする事を暗黙の前提としている．従って，上記の周波数伝達関数は式 (12‑10) に示した離散時間フーリエ変換 (DTFT) の定義式と等価となる．

一方，FIR フィルタはインパルス応答 h [n] を h [N − 1] で打ち切るため，FIR フィルタによって得られる現実の周波数伝達関数 H (e ^jωT) は以下で与えられる．

$$\begin{array}{}\text{(13-4)}& H\left(e^{j\omega T}\right)=\sum _{n=0}^{N-1}h\left[n\right]e^{-jn\omega T}\end{array}$$

ここで，インパルス応答を打ち切る事は，離散時間フーリエ変換 (DTFT) の総和 H_d (e ^jωT) を部分和 H (e ^jωT) で近似する事と等価となる．12.2 に述べた通り，フーリエ級数と離散時間フーリエ変換 (DTFT) は時間と角周波数と入れ替えた関係にあるから，この近似によって FIR フィルタの周波数特性には，8.1 に述べたギブスの現象に起因するリップルが生じる．

13.2. 基本的な FIR フィルタの例

11.2 の例と同じインパルス応答 h [n] に基づいた FIR フィルタの例を示す．これは，時定数 τ のローパスフィルタのインパルス応答を周期 T でサンプリングしたものである．式 (11‑8) に示したインパルス応答 h [n] を以下に再掲する．

$$\begin{array}{}\text{(13-5)}& h\left[n\right]=\frac{1}{\tau }{e}^{-\frac{nT}{\tau }},\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(n\ge 0\right)\end{array}$$

上記のインパルス応答に基づいた FIR フィルタのシステム伝達関数 H (z) を以下に示す．カットオフ周波数は ω_c = 1 / τ とする．また，FIR フィルタの次数 (レジスタ数) はN − 1 とする．

$$\begin{array}{}\text{(13-6)}& H\left(z\right)=\sum _{n=0}^{N-1}h\left[n\right]z^{-n}=\frac{1}{\tau }\sum _{n=0}^{N-1}{e}^{-\frac{nT}{\tau }}{z}^{-n}={\omega }_c\sum _{n=0}^{N-1}{e}^{-n{\omega }_{c}T}{z}^{-n}\end{array}$$

上記のシステム伝達関数の直流におけるゲインを 1 倍とした正規化システム伝達関数は H_N (z) 以下で与えられる．(式の展開は省略，等比級数の和の公式を使用，以下同様)．

$$\begin{array}{}\text{(13-7)}& H_N\left(z\right)=\frac{H\left(z\right)}{\underset{z\to 1}{\lim }H\left(z\right)}=\frac{1-e^{-{\omega }_{c}T}}{1-e^{-N{\omega }_{c}T}}\sum _{n=0}^{N-1}{e}^{-n{\omega }_{c}T}{z}^{-n}\end{array}$$

上記の正規化システム伝達関数に対応する，周波数伝達関数を以下に示す．(式の展開は省略)．

$$\begin{array}{}\text{(13-8)}& \begin{array}{}\begin{array}{r}{H}_N\left(e^{j\omega T}\right)\\ \end{array}\begin{array}{l}=\frac{1-e^{-{\omega }_{c}T}}{1-e^{-N{\omega }_{c}T}}\sum _{n=0}^{N-1}{e}^{-n{\omega }_{c}T}{e}^{-jn\omega T}\\ =\frac{\left(1-e^{-{\omega }_{c}T}\right)}{\left(1-e^{-N{\omega }_{c}T}\right)}\frac{\left\{1-e^{-N\left({\omega }_{c}T+j\omega T\right)}\right\}}{\left\{1-e^{-\left({\omega }_{c}T+j\omega T\right)}\right\}}\end{array}\end{array}\end{array}$$

N = 16 の場合の上記の周波数伝達関数のボード線図を図13‑2に示す．横軸の角周波数は ω / ω_c として正規化されている．図中の青線は正規化されたナイキスト周波数 fn を示しており，この例ではカットオフ周波数 ω_c の 20 倍の角周波数としている．また，図中の赤線はアナログフィルタの特性を示す．

図13-2: FIR によるローパスフィルタのボード線図の例．

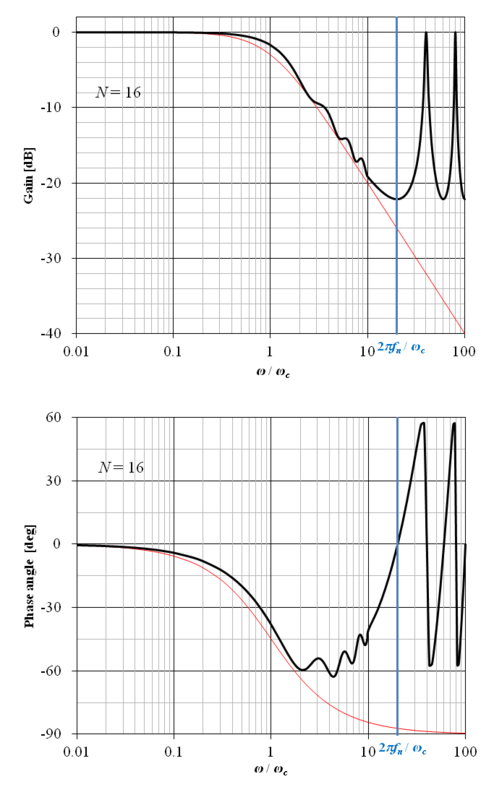
図から明らかな通り，ゲイン線図，位相線図共に，インパルス応答の打ち切りによって生じるギブスの現象のため，周波数特性が波打つリップルが生じている．

13.3. 窓関数による FIR フィルタの例

8.1 に示した通り，窓関数によってギブスの現象に起因するリップルを抑制する事が出来るため，上記の FIR フィルタにハミング窓を適用した例を示す．この例では n = 0 周辺の項の重み付を高くする必要があるため，式 (8‑17) で定義した以下のハミング窓を適用する．

$$\begin{array}{}\text{(13-9)}& w\left[n\right]=0.54+0.46\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\pi n}{N-1}\right),\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(0\le n\le N-1\right)\end{array}$$

この場合のインパルス応答 h [n] は以下で与えられる．

$$\begin{array}{}\text{(13-10)}& h\left[n\right]=\frac{1}{\tau }\left\{0.54+0.46\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\pi n}{N-1}\right)\right\}{e}^{-\frac{nT}{\tau }},\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(n\ge 0\right)\end{array}$$

上記のハミング窓を適用したインパルス応答に基づいた FIR フィルタのシステム伝達関数 H (z) を以下に示す．(式の展開は省略)．

$$\begin{array}{}\text{(13-11)}& \begin{array}{}\begin{array}{r}H\left(z\right)\\ \end{array}\begin{array}{l}=\sum _{n=0}^{N-1}{h\left[n\right]z}^{-n}\\ ={\omega }_c\left[0.54\left(\sum _{n=0}^{N-1}{e}^{-n{\omega }_{c}T}{z}^{-n}\right)+0.23\sum _{n=0}^{N-1}\left\{e^{-n\left({\omega }_{c}T-\frac{j\pi }{N-1}\right)}+e^{-n\left({\omega }_{c}T+\frac{j\pi }{N-1}\right)}\right\}{z}^{-n}\right]\end{array}\end{array}\end{array}$$

上記のシステム伝達関数の直流におけるゲインを 1 倍とした正規化システム伝達関数は以下で与えられる．(式の展開は省略)．

$$\begin{array}{}\text{(13-12)}& \begin{array}{}\begin{array}{c}{H}_N\left(z\right)=\frac{H\left(z\right)}{\underset{z\to 1}{\lim }H\left(z\right)}\\ \underset{z\to 1}{\lim }H\left(z\right)={\omega }_c\left[0.54\frac{1-e^{-N{\omega }_{c}T}}{1-e^{-{\omega }_{c}T}}+0.23\left\{\frac{{1-e}^{-N\left({\omega }_{c}T-\frac{j\pi }{N-1}\right)}}{{1-e}^{-\left({\omega }_{c}T-\frac{j\pi }{N-1}\right)}}+\frac{{1-e}^{-N\left({\omega }_{c}T+\frac{j\pi }{N-1}\right)}}{{1-e}^{-\left({\omega }_{c}T+\frac{j\pi }{N-1}\right)}}\right\}\right]\end{array}\end{array}\end{array}$$

上記の正規化システム伝達関数に対応する周波数伝達関数を以下に示す．(式の展開は省略)．

上記の周波数伝達関数のボード線図を図13‑3に示す．図13‑2と同様に N = 16 であり，横軸の角周波数は ω / ω_c として正規化されている．また図中の青線は正規化されたナイキスト周波数 fn を示しており，カットオフ周波数 ω_c の 20 倍の角周波数としている．

図13-3: 窓関数による FIR フィルタのボード線図の例．

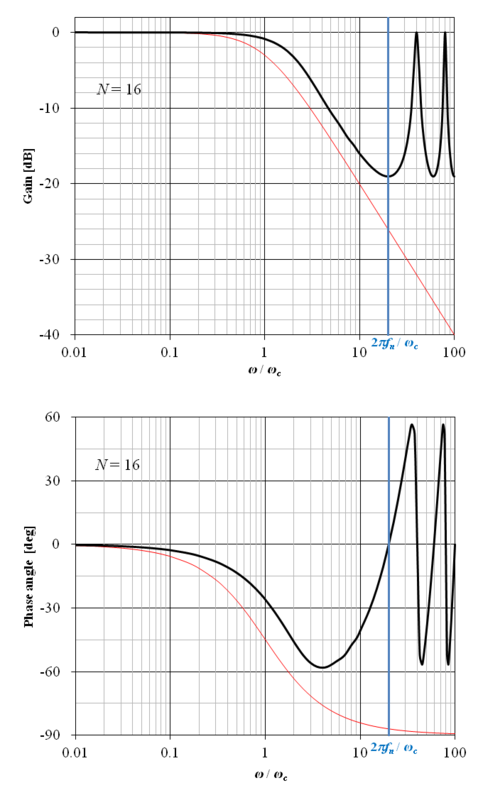
図から明らかな通り，ゲイン線図，位相線図共に，ハミング窓によって周波数特性のリップルが大幅に抑制されている．その反面，ハミング窓による重み付の影響で，減衰量が低下している．

以上より，IIR フィルタで出来る事を FIR フィルタで実現する事はあまりお勧めできない．11.2 に述べた IIR によるローパスフィルタに必要なレジスタ数は，式 (11‑11) の差分方程式から明らかな通り，僅か 1 個である．一方，上記の FIR フィルタの次数，即ちレジスタ数は N − 1 = 15 個となる．これはフィルタをハードウエアで実現する場合は論理回路のリソース数，ソフトウエアで実現する場合は実行時間に大幅な差が生じる事を示している．また，上記から明らかな通り FIR フィルタの設計は IIR フィルタと比較して煩雑である．従って，FIR フィルタが本領を発揮するのは，次に述べる線形位相 FIR フィルタの様な IIR フィルタでは実現できない特性のフィルタとなる．

13.4. 線形位相 FIR フィルタの基本

8.2 に述べた通り，正弦波を合成した際に得られる波形は，各正弦波の振幅と初期位相に依存する．従って，フィルタのゲイン特性が角周波数によらず 1 倍であっても，信号の遅延時間が角周波数によって異なる場合は，入力信号と異なる波形の出力信号が得られる．これを位相歪と呼ぶ．理想的にはフィルタの位相特性は角周波数によらず 0，即ち位相の進み遅れが無い零位相特性となる事が望ましい．しかし，この様なフィルタを実現する事は出来ないため，位相歪を避ける必要がある場合は，フィルタの遅延時間が角周波数によらず一定となる線形位相 (直線位相) 特性のフィルタが用いられる．

零位相特性フィルタ

位相特性が角周波数によらず 0 となる零位相特性フィルタの直感的な原理を説明する．インパルス応答を h [n] (n ≥ 0)，離散時間信号 x [n], y [n], (n ≥ 0) を入出力とするディジタルフィルタを考える．この場合，離散時間信号 x [n], y [n] の関係は，以下の畳み込みで記述される．また，入出力の離散時間信号 x [n], y [n] の周波数成分の間には，周波数伝達関数の位相特性に応じた位相の遅れ進みが生じる．

$$\begin{array}{}\text{(13-14)}& y\left[n\right]=\sum _{k=0}^{\infty }h\left[k\right]\mathrm{<mspace\; width="0.1em"></mspace>}x\left[n-k\right]\end{array}$$

ここで，入力の離散時間信号 x [n] の時間を逆順にした離散時間信号 rx [n] = x [−n], (0 ≥ n) を考える．この離散時間信号 rx [n] を上記のフィルタの入力とし，出力の離散時間信号を ry [n], (0 ≥ n) とすると，rx [n], ry [n] の関係は，以下の畳み込みで記述される．また，入出力の離散時間信号 rx [n], ry [n] の周波数成分の間には，上記と同じ位相の遅れ進みが生じる．

$$\begin{array}{}\text{(13-15)}& ry\left[n\right]=\sum _{k=0}^{\infty }h\left[k\right]\mathrm{<mspace\; width="0.1em"></mspace>}rx\left[n-k\right]=\sum _{k=0}^{\infty }h\left[k\right]\mathrm{<mspace\; width="0.1em"></mspace>}x\left[-n+k\right]\end{array}$$

次に，これらの離散時間信号 rx [n], ry [n] の時間を逆順にした離散時間信号 rrx [n] = rx [−n] 及び rry [n] = ry [−n], (n ≥ 0) を考える．ここで rrx [n] = x [n] は明らかである．よって，離散時間信号 x [n] と rry [n] の周波数成分の間には，上記と逆の位相の遅れ進みが生じる．従って，入力の離散時間信号 x [n] と y [n] + rry [n] の周波数成分の間には位相の遅れや進みは生じない．

ここで，h [n] の時間を逆順とした理論上，想像上のインパルス応答を rh [n] = h [−n], (0 ≥ n) とすると，上記の離散時間信号 x [n], rry [n] の関係は，以下の畳み込みで記述される．

$$\begin{array}{}\text{(13-16)}& rry\left[n\right]=ry\left[-n\right]=\sum _{k=0}^{\infty }h\left[k\right]\mathrm{<mspace\; width="0.1em"></mspace>}x\left[n+k\right]=\sum _{k=-\infty }^{0}rh\left[k\right]\mathrm{<mspace\; width="0.1em"></mspace>}x\left[n-k\right]\end{array}$$

上記の式から明らかな通り，散時間信号 rry [n] は，入力の離散時間信号 x [n] と rh [n] = h [−n] の畳み込みから得られる．よって，入力の離散時間信号を x [n]，インパルス応答を h [n] + rh [n] = h [n] + h [−n] とするフィルタの出力の離散時間信号は y [n] + rry [n] となる．

従って，入力の離散時間信号を x [n], (n ≥ 0)，出力の離散時間信号を y [n]，理論上，想像上のインパルス応答を h_d [n] = h_d [−n] とするフィルタの入出力の関係は以下の畳み込みで記述され，この入出力の離散時間信号間には位相の進みや遅れは生じず，即ち位相特性は角周波数によらず 0 となる．このため，想像上，理論上のインパルス応答が h_d [n] = h_d [−n] となるフィルタの位相特性は零位相特性となる．

$$\begin{array}{}\text{(13-17)}& y\left[n\right]=\sum _{k=-\infty }^{\infty }{h}_d\left[k\right]\mathrm{<mspace\; width="0.1em"></mspace>}x\left[n-k\right]\end{array}$$

線形位相 (直線位相) FIR フィルタ

残念ながら，13.1 に述べた通り，ディジタル信号処理のインパルス応答は h [n] = 0, (n < 0) でなければならないため，零位相特性フィルタを実現する事は出来ない．しかし，FIR フィルタでは，信号の遅延時間が角周波数によらず一定となり，位相歪が生じない線形位相 (直線位相) 特性を実現する事ができる．零位相特性となるインパルス応答 h_d [n] に対して，以下のインパルス応答 h [n] を考える．ここで，N は奇数とする．

$$\begin{array}{}\text{(13-18)}& h\left[n\right]=\left\{\begin{array}{l}{h}_d\left[n-\frac{N-1}{2}\right],\mathrm{<mspace\; width="0.2em"></mspace>}\left(0\le n\le N-1\right)\\ 0,\mathrm{<mspace\; width="6.8em"></mspace>}\left(n<0,\mathrm{<mspace\; width="0.2em"></mspace>}n\ge N\right)\end{array}\right.\end{array}$$

上記から明らかな通り，h [n] は，h_d [n] を |n| ≤ (N − 1) / 2 で打ち切り，かつ (N − 1) / 2 サンプル時間遅延させたインパルス応答となる．ここで，h_d [n] = h_d [−n] であるから，h [n] には以下の関係が成立する．

$$\begin{array}{}\text{(13-19)}& h\left[n\right]=h\left[N-1-n\right],\mathrm{<mspace\; width="0.2em"></mspace>}\left(0\le n\le N-1\right)\end{array}$$

従って，インパルス応答 h [n] が式 (13‑19) を満たす FIR フィルタの遅延時間は角周波数よらず一定となり，線形位相特性となる．線形位相 FIR フィルタの構造を図13‑4 に示す．

図13-4: 線形位相 FIR フィルタの構造．

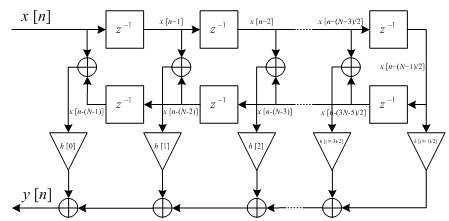
Note: N が偶数の場合でも，インパルス応答が式 (13‑19) を満たす FIR フィルタは線形位相特性となる．尚，この場合の FIR フィルタの構造は図13‑4 とは若干異なる形となる．

Note: 信号の遅延時間が周波数によらず一定となる事は，時間軸のシフトやむだ間要素と等価であり，位相遅れが角周波数に比例するため，線形位相 (直線位相) 特性と呼ばれる．

以上の線形位相特性とは，あくまで FIR フィルタのシステム伝達関数や周波数伝達関数における特性である事に注意せよ．現実のディジタ信号処理システムでは，サンプラーの前に異名現象を低減させるローパスフィルタが設けられている場合はこれの位相特性，また 10.6 に述べた 0 次ホールドの位相特性が加わるため，これらを含めた現実のディジタル信号処理システムにおける線形位相特性の実現には高度な技法が必要となる．

13.5. 理想的ローパスフィルタのインパルス応答

式 (13‑19) を満たすインパルス応答の例として，理想的ローパスフィルタのインパルス応答を示す．このフィルタの周波数伝達関数は以下で与えられる．ここで，ω_c はカットオフ周波数，T はサンプリング周期を示す．即ち「理想的」ローパスフィルタとは カットオフ周波数を超える周波数成分を全く含まないフィルタの事である．

$$\begin{array}{}\text{(13-20)}& H_d\left(e^{j\omega T}\right)=\left\{\begin{array}{l}1,\mathrm{<mspace\; width="0.2em"></mspace>}\left(\left|\omega \right|\le {\omega }_c\right)\\ 0,\mathrm{<mspace\; width="0.2em"></mspace>}\left({\omega }_c<\left|\omega \right|\le \pi /T\right)\end{array}\right.\end{array}$$

上記の周波数伝達関数と式 (12‑11) に示した離散時間フーリエ変換 (DTFT) の逆変換から，理想的ローパスフィルタのインパルス応答 h_d [n] を求める．

$$\begin{array}{}\text{(13-21)}& \begin{array}{c}\begin{array}{r}{h}_d\left[n\right]\\ \\ \\ \end{array}\begin{array}{l}=\frac{T}{2\pi }{\int }_{-\frac{\pi }{T}}^{\frac{\pi }{T}}{H}_d\left(e^{j\omega T}\right)\mathrm{<mspace\; width="0.1em"></mspace>}{e}^{jn\omega T}d\omega \\ =\frac{T}{2\pi }{\int }_{-{\omega }_c}^{{\omega }_c}\mathrm{<mspace\; width="0.1em"></mspace>}{e}^{jn\omega T}d\omega \\ =\frac{1}{\pi n}\frac{e^{jn{\omega }_{c}T}-e^{-jn{\omega }_{c}T}}{j2}\\ =\frac{1}{\pi n}\mathrm{s}\mathrm{i}\mathrm{n}\left(n{\omega }_{c}T\right),\mathrm{<mspace\; width="0.2em"></mspace>}\left(n\ne 0\right)\end{array}\\ h_d\left[n\right]=\frac{T}{2\pi }{\int }_{-{\omega }_c}^{{\omega }_c}\mathrm{<mspace\; width="0.1em"></mspace>}{e}^{jn\omega T}d\omega =\frac{{\omega }_{c}T}{\pi },\mathrm{<mspace\; width="0.2em"></mspace>}\left(n=0\right)\end{array}\end{array}$$

正弦関数は奇関数であるから，理想的ローパスフィルタのインパルス応答は h_d [n] = h_d [−n] となり，このフィルタの位相特性は零位相特性となる．

次に，上記のインパルス応答 h_d [n] を |n| ≤ (N − 1) / 2 で打ち切り，かつ (N − 1) / 2 サンプル時間遅延させインパルス応答 h [n] を以下に示す．

$$\begin{array}{}\text{(13-22)}& h\left[n\right]=\left\{\begin{array}{l}\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left\{\left(n-\frac{N-1}{2}\right){\omega }_{c}T\right\}}{\pi \left(n-\frac{N-1}{2}\right)},\mathrm{<mspace\; width="0.2em"></mspace>}\left(0\le n\le N-1,\mathrm{<mspace\; width="0.2em"></mspace>}n\ne \frac{N-1}{2}\right)\\ \frac{{\omega }_{c}T}{\pi },\mathrm{<mspace\; width="8em"></mspace>}\left(\mathrm{<mspace\; width="0.1em"></mspace>}n=\frac{N-1}{2}\right)\\ 0,\mathrm{<mspace\; width="10em"></mspace>}\left(n<0,\mathrm{<mspace\; width="0.2em"></mspace>}n\ge N\right)\end{array}\right.\end{array}$$

上記は，式 (13‑19) を満たすため，インパルス応答を h [n] とする FIR フィルタは線形位相特性となる．

Note: 上記は N が奇数，偶数に係わらず成立する．

13.6. 線形位相 FIR フィルタの例

式 (13‑22) に示したインパルス応答に基づいた FIR フィルタのシステム伝達関数 H (z) を以下に示す．この FIR フィルタの次数は N − 1 となる．

$$\begin{array}{}\text{(13-23)}& H\left(z\right)=\sum _{n=0}^{N-1}h\left[n\right]z^{-n}\end{array}$$

上記のシステム伝達関数に対応する，周波数伝達関数を以下に示す．

$$\begin{array}{}\text{(13-24)}& H\left(e^{j\omega T}\right)=\sum _{n=0}^{N-1}h\left[n\right]e^{-jn\omega T}\end{array}$$

ω_cT = π / 2 の場合の上記の周波数伝達関数のゲイン線図を図13‑5に示す．図は N = 7, 11, 19, 35, 67 の場合の例を示している．横軸の角周波数は ωT として正規化されている．また，上の図の縦軸のゲインは dB 表示，下の図の縦軸のゲインは比による表示となっている．

図13-5: 線形位相 FIRフィルタのゲイン線図の例．

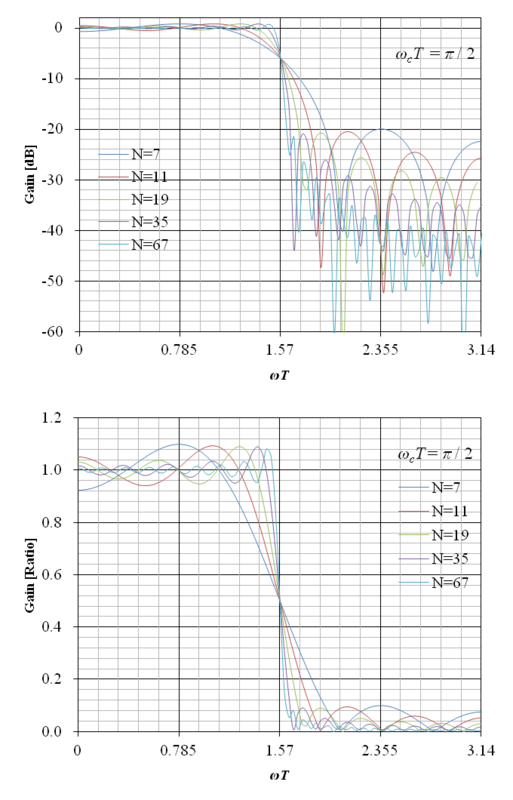
縦軸を比としたゲイン線図から明らかな通り，インパルス応答の打ち切りによって生じるギブスの現象により，ゲイン特性が波打つリップルが生じている．8.1に方形波のフーリエ級数の総和を部分和で近似した際に，ギブスの現象によって生じるリップルを示したが，上記の例の理想的ローパスフィルタのゲイン特性は，角周波数に対して方形状の特性となるため，これを近似した FIR フィルタのゲイン特性には 8.1と同様なリップルが生じる．また，縦軸を dB としたゲイン線図から明らかな通り，特に ωT > π / 2 となる周波数領域におけるゲイン特性のリップルのため，理想的ローパスフィルタと比較して，得られる減衰量に高い誤差が生じる．

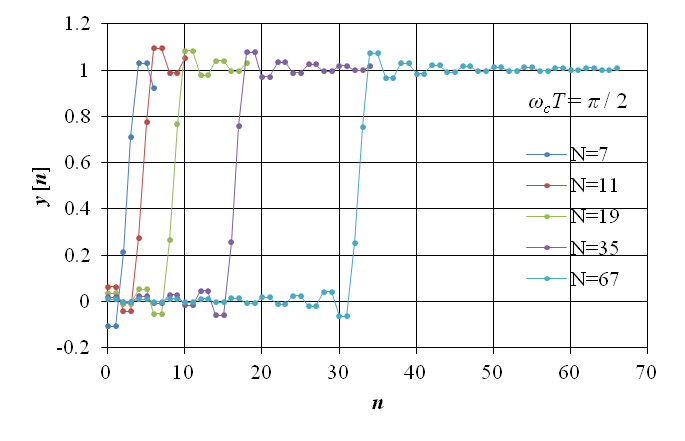
このフィルタの入力の離散時間信号を x [n] = u [n] とした際の，インディシャル応答 (単位ステップ応答) y [n] を図13‑6 に示す．図から明らかな通り，このフィルタのインディシャル応答には，フィルタの次数 (レジスタ数) に比例した遅延が加わり，不連続点近傍で振動的となるリップルが生じている．

図13-6: 線形位相 FIRフィルタのインディシャル応答の例．

13.7. 窓関数による線形位相 FIR フィルタの例

8.1 に示した通り，窓関数によってギブスの現象に起因するリップルを抑制する事が出来るため，上記の線形位相 FIR フィルタのインパルス応答にハミング窓を適用した例を示す．この例では n = (N − 1) / 2 周辺の項の重み付を高くする必要があるため，式 (8‑16) で定義した以下のハミング窓を適用する．

$$\begin{array}{}\text{(13-25)}& w\left[n\right]=0.54-0.46\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{2\pi n}{N-1}\right),\mathrm{<mspace\; width="0.1em"></mspace>}\mathrm{<mspace\; width="0.1em"></mspace>}\left(0\le n\le N-1\right)\end{array}$$

式 (13‑22) に示したインパルス応答に上記のハミング窓を適用した FIR フィルタのシステム伝達関数 H (z) を以下に示す．

$$\begin{array}{}\text{(13-26)}& H\left(z\right)=\sum _{n=0}^{N-1}w\left[n\right]h\left[n\right]z^{-n}\end{array}$$

上記のシステム伝達関数の直流におけるゲインを 1 倍とした正規化システム伝達関数 H_N (z) は以下で与えられる．

$$\begin{array}{}\text{(13-27)}& H_N\left(z\right)=\frac{H\left(z\right)}{\underset{z\to 1}{\lim }H\left(z\right)}=\frac{1}{\underset{z\to 1}{\lim }H\left(z\right)}\sum _{n=0}^{N-1}w\left[n\right]h\left[n\right]z^{-n}\end{array}$$

上記の正規化システム伝達関数に対応する，周波数伝達関数を以下に示す．

$$\begin{array}{}\text{(13-28)}& H_N\left(e^{j\omega T}\right)=\frac{1}{\underset{z\to 1}{\lim }H\left(z\right)}\sum _{n=0}^{N-1}w\left[n\right]h\left[n\right]e^{-jn\omega T}\end{array}$$

ω_cT = π / 2 の場合の上記の周波数伝達関数のゲイン線図を図13‑7に示す．横軸の角周波数は ωT として正規化されている．また，上の図の縦軸は dB 表示，下の図の縦軸は比による表示となっている．

図13-7: 窓関数による線形位相 FIRフィルタのゲイン線図の例1．

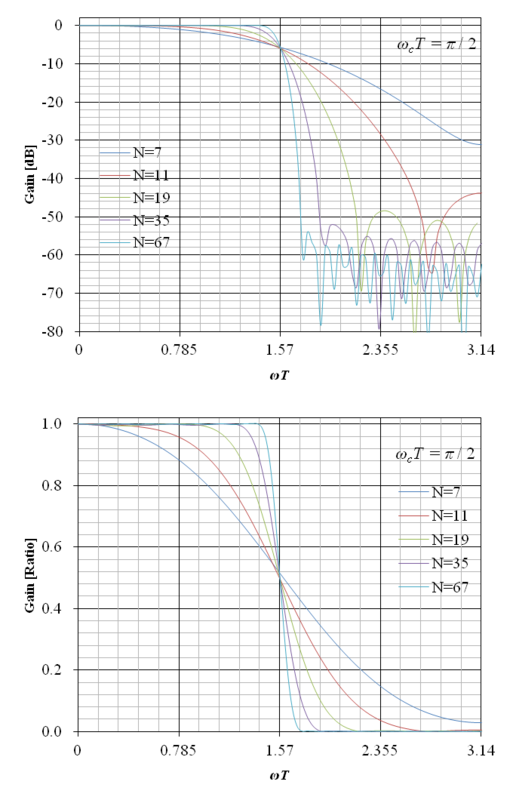
図から明らかな通り，ハミング窓によってゲイン特性のリップルが大幅に抑制されて，減衰量が大幅に高くなっている．但し，ハミング窓による重み付の影響により，減衰傾斜は緩やかになっている．

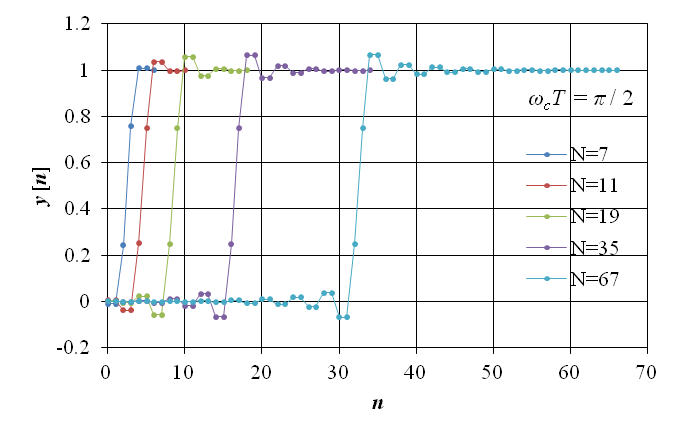
また，このフィルタのインディシャル応答 y [n] を図13‑8に示す．図から明らかな通り，インディシャル応答には不連続点近傍で振動的となるリップルが生じている．この，リップルの幅はハミング窓が無い場合よりわずかに低くなっているが，ゲイン特性のリップルと異なり，インディシャル応答のリップルはハミング窓によって大幅には改善されない．

図13-8: 窓関数による線形位相 FIRフィルタのインディシャル応答の例1．

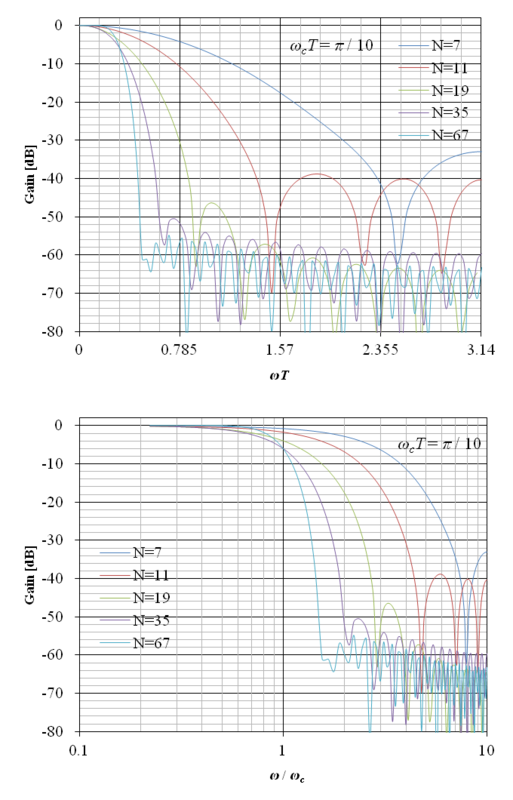
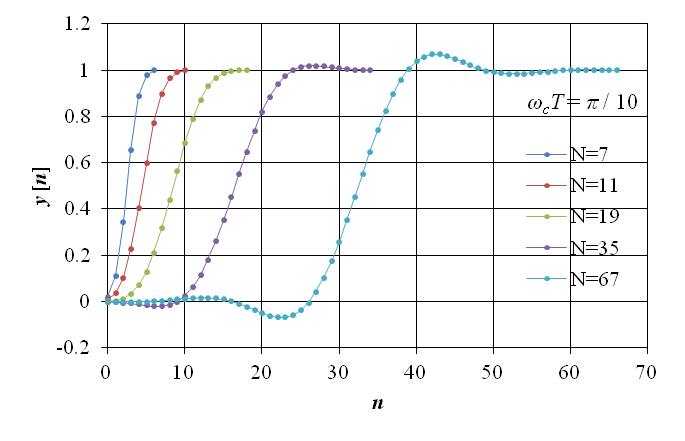
以上の線形位相 FIR フィルタのゲイン線図の例は多くの教科書に示されているが，フィルタの特徴を端的に示すためにカットオフ周波数を ω_cT = π / 2 ，即ちナイキスト周波数の 1 / 2 にしている様に見受けられるため，参考として ω_cT = π / 10 の場合の周波数伝達関数のゲイン線図を図13‑9に示す．上の図の横軸の角周波数は ωT として正規化されている．また，下の図の横軸の角周波数は，アナログフィルタのゲイン線図の慣例に合わせ ω / ω_c として正規化され，対数軸で表示されている．ここで ω / ω_c = 1 は正規化されたカットオフ周波数を示す．また，この場合のインディシャル応答 y [n] を図13‑10に示す．

図13-9: 窓関数による線形位相 FIRフィルタのゲイン線図の例2．

図13-10: 窓関数による線形位相 FIRフィルタのインディシャル応答の例2．

本章の参考文献

A. Oppenheim, R. Schafer, 伊達訳, "ディジタル信号処理," (上), (下), コロナ社, 1978.