8. フーリエ級数展開とフーリエ変換

本章はフーリエ級数展開とフーリエ変換について述べる．これらフーリエ解析は振動の分析に適用する事ができ，線形時不変システムより広い分野で利用されているため，非常に多くの教科書がある．このため，本資料では数式の証明や導出は省略し，振動の分析という観点からの解説を行う．尚，フーリエ解析における種々の関係は，以下の f (t) が複素数の場合でも成立するが，その物理的な意味を見い出す事は容易ではないため，本資料では扱わない．

8.1. フーリエ級数展開
8.2. フーリエ変換

8.1. フーリエ級数展開

周期 2π の周期関数のフーリエ級数展開

f (t) を区間 [−π, π] で定義された周期 2π の周期関数とすると，以下の式に示す通り，f (t) は定数，及び周期 2π / n, (n = 1, 2, 3, ...) の正弦関数，及び余弦関数の和から成るフーリエ級数で表す事ができる．下記の式の ~ は，フーリエ級数が厳密に f (t) に収束する場合と，近似となる場合がある事を示している．

$\begin{matrix} (8-1) & f (t) ~ \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} a_{n} \cos (n t) + b_{n} \sin (n t) \end{matrix}$

ここで，a_n 及び b_n はフーリエ係数と呼ばれ，以下で与えられる．

$\begin{matrix} (8-2) & \begin{matrix} \begin{matrix} a_{n} = \frac{1}{π} \int_{- π}^{π} f (t) c o s (n t) d t, (n = 0, 1, 2, \dots) \\ b_{n} = \frac{1}{π} \int_{- π}^{π} f (t) s i n (n t) d t, (n = 1, 2, 3, \dots) \end{matrix} \end{matrix} \end{matrix}$

以上がフーリエ級数展開の教科書的定義である．ここで，式 (1-14) に示した三角関数の合成定理によって，式 (8-1) は以下の通り変形できる．

$\begin{matrix} (8-3) & \begin{matrix} \begin{matrix} f (t) ~ \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} a_{n} \cos (n t) + b_{n} \sin (n t) = \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} A_{n} s i n (n t + φ_{n}) \\ A_{n} = \sqrt{{a_{n}}^{2} + {b_{n}}^{2}}, φ_{n} = {t a n}^{- 1} \frac{a_{n}}{b_{n}}, (n = 1, 2, 3, \dots) \end{matrix} \end{matrix} \end{matrix}$

即ち，f (t) を時間 [−π, π] で定義された周期 2π の振動における変位とすると，上記は角周波数が n，振幅が A_n，初期位相が φ_n, (n = 1, 2, 3, ...) となる正弦波と，直流成分 a₀ / 2の重ね合わせで f (t) を表せる事を示している．

式 (8‑2) のフーリエ係数を，以下の式に基づいて，複素フーリエ係数に変換すると，複素フーリエ級数が得られる．

$\begin{matrix} (8-4) & c_{0} = \frac{a_{0}}{2}, c_{n} = \frac{a_{n} - j b_{n}}{2}, c_{- n} = \overline{c_{n}} = \frac{a_{n} + j b_{n}}{2} \end{matrix}$

複素フーリエ級数と複素フーリエ係数を以下に示す．これらは，式 (8-1) 及び (8-2) の別表現となる．

$\begin{matrix} (8-5) & \begin{matrix} \begin{matrix} f (t) ~ \sum_{n = - \infty}^{\infty} c_{n} e^{j n t} \\ c_{n} = \frac{1}{2 π} \int_{- π}^{π} f (t) e^{- j n t} d t, (n = 0, \pm 1, \pm 2, \dots) \end{matrix} \end{matrix} \end{matrix}$

以上が，複素フーリエ級数展開の教科書的定義である．ここで，f (t) が実数の場合は c_n と c_−n は共役複素数の関係となるため，式 (8‑5) は以下の通り変形できる．

$\begin{matrix} (8-6) & \begin{matrix} \begin{array}{r} f (t) ~ \sum_{n = - \infty}^{\infty} c_{n} e^{j n t} \end{array} \begin{array}{l} = c_{0} + \sum_{n = 1}^{\infty} (c_{n} e^{j n t} + \overline{c_{n}} e^{- j n t}) \\ = c_{0} + \sum_{n = 1}^{\infty} \frac{j 2 c_{n} e^{j n t} - (- j 2 \overline{c_{n}} e^{- j n t})}{j 2} \end{array} \end{matrix} \end{matrix}$

ここで，A_n = | j2c_n| = 2 | c_n|, φ_n = Arg ( j2c_n) とすると，上記は更に以下の通り変形できる．

$\begin{matrix} (8-7) & \begin{matrix} \begin{array}{r} f (t) ~ \sum_{n = - \infty}^{\infty} c_{n} e^{j n t} \end{array} \begin{array}{l} = c_{0} + \sum_{n = 1}^{\infty} A_{n} \frac{e^{j φ_{n}} e^{j n t} - e^{- j φ_{n}} e^{- j n t}}{j 2} \\ = c_{0} + \sum_{n = 1}^{\infty} A_{n} \frac{e^{j (n t + φ_{n})} - e^{- j (n t + φ_{n})}}{j 2} \end{array} \\ {A_{n} = |j 2 c_{n}| = 2 |c_{n}|, φ}_{n} = A r g (j 2 c_{n}), (n = 1, 2, 3, \dots) \\ c_{n} = \frac{1}{2 π} \int_{- π}^{π} f (t) e^{- j n t} d t, (n = 0, 1, 2, \dots) \end{matrix} \end{matrix}$

上記の複素フーリエ級数の総和における各項は，式 (2‑27) に示した複素指数関数による正弦波の記述となる．よって，f (t) を時間 [−π, π] で定義された周期 2π の振動における変位とすると，上記は角周波数が n，振幅が A_n，初期位相が φ_n, (n = 1, 2, 3, ...) となる正弦波と，直流成分 c₀ の重ね合わせで f (t) を表せる事を示している．

Note: 上記の直流成分は c₀となるが，正弦波の振幅は 2 | c_n| となる事に注意せよ．フーリエ級数に限らず，フーリエ解析を正弦波と直流成分の重ね合わせとして解釈する場合，直流成分と正弦波は区別して扱わなければならない．

周期 2L の周期関数のフーリエ級数展開

f (t) を区間 [−L, L] で定義された周期 2L の周期関数とすると，以下の式に示す通り，f (t) は定数，及び周期 2L / n, (n = 1, 2, 3, ...) の正弦関数，及び余弦関数の和から成るフーリエ級数で表す事ができる．

$\begin{matrix} (8-8) & f (t) ~ \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} a_{n} \cos (\frac{n π t}{L}) + b_{n} \sin (\frac{n π t}{L}) \end{matrix}$

フーリエ係数 a_n 及び b_n は以下で与えられる．

$\begin{matrix} (8-9) & \begin{matrix} \begin{matrix} a_{n} = \frac{1}{L} \int_{- L}^{L} f (t) c o s (\frac{n π t}{L}) d t, (n = 0, 1, 2, \dots) \\ b_{n} = \frac{1}{L} \int_{- L}^{L} f (t) s i n (\frac{n π t}{L}) d t, (n = 1, 2, 3, \dots) \end{matrix} \end{matrix} \end{matrix}$

また，上記の別表現となる複素フーリエ級数と複素フーリエ係数を以下に示す．

$\begin{matrix} (8-10) & \begin{matrix} \begin{matrix} f (t) ~ \sum_{n = - \infty}^{\infty} c_{n} e^{j \frac{n π t}{L}} \\ c_{n} = \frac{1}{2 L} \int_{- L}^{L} f (t) e^{- j \frac{n π t}{L}} d t, (n = 0, \pm 1, \pm 2, \dots) \end{matrix} \end{matrix} \end{matrix}$

以上の教科書的定義において L = π / ω と置き換えると，f (t) は区間 [−π / ω, π / ω] で定義された周期 2π / ω の周期関数となる．この場合，f (t) を時間 [−π / ω, π / ω] で定義された周期 2π / ω の振動における変位とすると，f (t) は，以下の通り，角周波数が nω，振幅が A_n，初期位相が φ_n, (n = 1, 2, 3, ...) となる正弦波と，直流成分 a₀ / 2の重ね合わせで表す事ができる．

$\begin{matrix} (8-11) & \begin{matrix} \begin{matrix} a_{n} = \frac{ω}{π} \int_{- π / ω}^{π / ω} f (t) c o s (n ω t) d t, (n = 0, 1, 2, \dots) \\ b_{n} = \frac{ω}{π} \int_{- π / ω}^{π / ω} f (t) s i n (n ω t) d t, (n = 1, 2, 3, \dots) \\ A_{n} = \sqrt{{a_{n}}^{2} + {b_{n}}^{2}}, φ_{n} = {t a n}^{- 1} \frac{a_{n}}{b_{n}}, (n = 1, 2, 3, \dots) \\ f (t) ~ \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} a_{n} \cos (n ω t) + b_{n} \sin (n ω t) = \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} A_{n} s i n (n ω t + φ_{n}) \end{matrix} \end{matrix} \end{matrix}$

また，式 (8‑10) の f (t) が実数の場合は c_n と c_−n は共役複素数の関係となるため，式 (8‑10) の複素フーリエ級数と複素フーリエ係数は以下の通り変形できる．

$\begin{matrix} (8-12) & \begin{matrix} \begin{matrix} c_{n} = \frac{ω}{2 π} \int_{- π / ω}^{π / ω} f (t) e^{- j n ω t} d t \\ {A_{n} = 2 |c_{n}|, φ}_{n} = A r g (j 2 c_{n}), (n = 1, 2, 3, \dots) \\ f (t) ~ \sum_{n = - \infty}^{\infty} c_{n} e^{j n ω t} = c_{0} + \sum_{n = 1}^{\infty} A_{n} \frac{e^{j (n ω t + φ_{n})} - e^{- j (n ω t + φ_{n})}}{j 2} \end{matrix} \end{matrix} \end{matrix}$

上記は角周波数が nω，振幅が A_n，初期位相が φ_n, (n = 1, 2, 3, ...) となる正弦波と，直流成分 c₀ の重ね合わせで f (t) を表せる事を示している．

フーリエ級数の収束

f (t) を区間 [a, b] で定義された周期関数とすると，f (t) が有限個の点を除いて連続であり，かつ全ての不連続点において，左側極限値と右側極限値が存在し，かつ a 及び b において各々左側極限値と右側極限値が存在する場合，f (t) を区分的に連続な関数と言う．また，周期関数 f (t) の導関数 f '(t) が区間 [a, b] において区分的に連続な関数となる場合，f (t) を区分的に滑らかな関数と言う．

区分的に連続，かつ区分的に滑らかな周期関数 f (t) のフーリエ級数の収束を以下に示す．

連続な点における f (t) のフーリエ級数は f (t) に収束する．
不連続な点における f (t) のフーリエ級数は，下記の通り，不連続点の左側極限値と右側極限値の平均に収束する．

$\begin{matrix} (8-13) & \frac{f (t - 0) + f (t + 0)}{2} \end{matrix}$

即ち，フーリエ級数は連続関数となる正弦波，及び直流成分の重ね合わせによって周期関数を表現するものであるため，連続な点は厳密に表現できるが，不連続点は近似となり，これを厳密に表現する事は出来ない．

ギブスの現象

f (t) が以下で与えられる周期 2π の方形波 (矩形波) のフーリエ級数を例に，不連続点におけるフーリエ級数の収束過程を示す．

$\begin{matrix} (8-14) & f (t) = \{\begin{array}{l} 1, (0 \leq t < π) \\ - 1, (- π \leq t < 0) \end{array} \end{matrix}$

上記の方形波のフーリエ級数は以下で与えられる．

$\begin{matrix} (8-15) & f (t) ~ \frac{4}{π} \sum_{n = 1}^{\infty} \frac{s i n \{(2 n - 1) t\}}{2 n - 1} \end{matrix}$

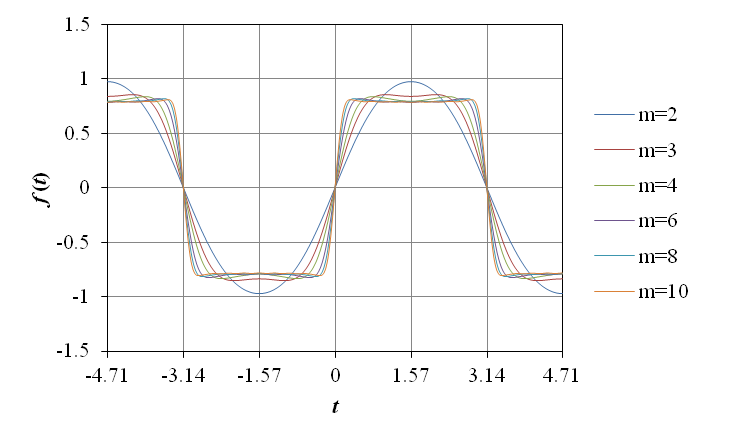
上記のフーリエ級数の総和を n = 1 から m までの部分和で近似した際のグラフを以下に示す．

f:id:suzumushi0:20170611122147p:plain — **図8-1: 方形波のフーリエ級数の収束．**

図から明らかな通り，m が増大するに伴い，正弦波の重ね合わせは方形波に近づき，f (t) に収束してゆく．但し，不連続点の近傍で振動的な現象が観察される．m を更に増大させ，不連続点の近傍を拡大した図を以下に示す．

f:id:suzumushi0:20170611122148p:plain — **図8-2: 方形波のフーリエ級数の収束(拡大)．**

図から明らかな通り，不連続点の近傍における振動的な現象は m が増大しても生じる．これはギブスの現象と呼ばれ，不連続点を含む周期関数のフーリエ級数の総和を部分和で近似した場合，不連続点の近傍で必ず生じる事が知られている．尚，不連続点 f (t) 近傍における，振動的な現象によるオーバーシュート，アンダーシュートの振幅は，不連続点の幅 f (t − 0) − f (t + 0) の約 0.09 倍となる．

以上が，ギブスの現象の教科書的説明である．ここで，振動の分析の観点からは，方形波のフーリエ級数の総和を部分和で近似する事は，方形波をローパスフィルタに通す事に等しい．従って，ギブスの現象は，カットオフ周波数を超える周波数成分を全く含まないローパスフィルタのインディシャル応答 (単位ステップ応答) や方形波の応答が，不連続点近傍で振動的となる事を示している．この振動はリップル (リンギング) と呼ばれる．

図6‑10 に示した通り，2 次遅れ要素のゲインは固有振動数 (共振周波数) 近傍で 0 [dB] 以上となるため，7.4 に示した通り，これのインディシャル応答が振動的となる事は直感的に理解できる．しかし，固有振動数を持たないローパスフィルタであっても，インディシャル応答が振動的となる場合がある事に十分留意する必要がある．事実，ローパスフィルタとして基本的な特性のバタワースフィルタは，次数を高くし減衰傾斜を急峻にすると，インディシャル応答や方形波の応答が振動的となり，リップルが生じる事が知られている．

リップルが生じるフィルタは，用途によっては許容されない場合がある．カットオフ周波数を超える周波数成分を全く含まないローパスフィルタは「理想的」フィルタと呼ばれ，またフィルタの減衰傾斜は急峻であるほど良い特性であるとの誤解が多く見受けられるが，過ぎたるは猶及ばざるが如し，その様な特性のフィルタは用途によっては問題を引き起こす可能性がある事に留意する必要がある．

窓関数によるリップルの抑制

リップルは，単純に減衰傾斜を緩やかにすれば抑制する事ができる．上に述べた方形波のフーリエ級数の総和を部分和で近似する場合は，部分和の各項に重み付の係数を乗じる事によってこれを実現できる．この様な重み付の技法は無数に存在するが，その代表的なものとして窓関数がある．最も良く使われる窓関数としてハミング窓を以下に示す．

$\begin{matrix} (8-16) & w [n] = 0.54 - 0.46 c o s (\frac{2 π n}{N - 1}), (0 \leq n \leq N - 1) \end{matrix}$

ここで，w [n] は項 n の重み付の係数，N は項数を示す．上記は，多くの教科書に示されているハミング窓の定義で，n = N / 2 を中心とした項の重み付を高くする場合の定義式となる．

上に述べた，方形波のフーリエ級数の総和を部分和で近似する場合は，n = 0 を周辺の項の重み付を高くする必要があり，この場合のハミング窓の定義式は以下で与えられる．

$\begin{matrix} (8-17) & w [n] = 0.54 + 0.46 c o s (\frac{π n}{N - 1}), (0 \leq n \leq N - 1) \end{matrix}$

よって，ハミング窓で重み付された，方形波のフーリエ級数における m 項までの部分和による近似は以下で与えられる．

$\begin{matrix} (8-18) & f (t) ≃ \frac{4}{π} \sum_{n = 1}^{m} \{0.54 + 0.46 c o s (\frac{π n}{m - 1})\} \frac{s i n \{(2 n - 1) t\}}{2 n - 1} \end{matrix}$

上記の計算結果のグラフを以下に示す．

f:id:suzumushi0:20170611122149p:plain — **図8-3: ハミング窓で重み付された方形波のフーリエ級数の収束．**

図から明らかな通り，ハミング窓による重み付により減衰傾斜が緩やかとなり，リップルは殆ど生じていない．その反面，重み付の影響により信号の立ち上がり，立下りに要する時間が長くなり，波形の変化が緩やかになっている．

8.2. フーリエ変換

フーリエ変換の定義

周期 2L の周期関数のフーリエ係数，フーリエ級数展開を L→∞ とする事によってフーリエ変換，フーリエ逆変換が得られる．区間 [−∞, ∞] で定義された関数 f (t) のフーリエ変換 F (ω) を以下に示す．

$\begin{matrix} (8-19) & F (ω) = \int_{- \infty}^{\infty} f (t) e^{- j ω t} d t \end{matrix}$

関数 f (t) とフーリエ変換 F (ω) の関係を以下の様に表示する場合もある．

$\begin{matrix} (8-20) & F [f (t)] = F (ω) \end{matrix}$

同様に，関数 f (t) は F (ω) のフーリエ逆変換とも呼ばれ，以下の式で表す事ができる．フーリエ級数と同様に，下記の式の ~ は，フーリエ逆変換が厳密に f (t) に収束する場合と，近似となる場合がある事を示している．

$\begin{matrix} (8-21) & f (t) ~ \frac{1}{2 π} \int_{- \infty}^{\infty} F (ω) e^{j ω t} d ω \end{matrix}$

上記の関係を以下の様に表示する場合もある．

$\begin{matrix} (8-22) & F^{- 1} [F (ω)] ~ f (t) \end{matrix}$

フーリエ変換，逆変換の定義式は，係数 1 / (2π) を除けば，t と ω を入れ替えただけで，実質的に同じ式となる．

Note: フーリエ変換，逆変換の定義式は分野や文献によって異なる．特に，係数 1 / (2π) を変換，逆変換のどちらの係数とするかに差異が見られる．フーリエ係数との整合性の観点から，係数 1 / (2π) をフーリエ変換の定義式の係数とする場合もある．また，フーリエ変換，逆変換の定義式の対称性，パーセバルの定理によるエネルギーの計算との整合性の観点から，係数 1 / (2π) の平方根を変換，逆変換双方の係数とする場合もある．本資料ではラプラス変換の定義式との整合性の観点から，上記の様に係数 1 / (2π) を逆変換の定義式の係数としている．

以上が，フーリエ変換の教科書的定義である．ここで，f (t) が実数の場合は F (ω) と F (−ω) は共役複素数の関係となるため，フーリエ逆変換の定義式 (8‑21) は以下の通り変形できる．

$\begin{matrix} (8-23) & \begin{matrix} f (t) ~ \frac{1}{2 π} \int_{- \infty}^{\infty} F (ω) e^{j ω t} d ω \\ \begin{array}{r} ∴ f (t) \end{array} \begin{array}{l} - \frac{F (0)}{2 π} ~ \frac{1}{2 π} \int_{0 +}^{\infty} F (ω) e^{j ω t} + \overline{F (ω)} e^{- j ω t} d ω \\ = \frac{1}{π} \int_{0 +}^{\infty} \frac{j F (ω) e^{j ω t} - \{- j \overline{F (ω)} e^{- j ω t}\}}{j 2} d ω \\ = \int_{0 +}^{\infty} A (ω) \frac{e^{j \{ω t + φ (ω)\}} - e^{- j \{ω t + φ (ω)\}}}{j 2} d ω \end{array} \\ A (ω) = |\frac{F (ω)}{π}|, φ (ω) = A r g \{j \frac{F (ω)}{π}\}, (ω > 0) \end{matrix} \end{matrix}$

即ち，f (t) を時間 [−∞, ∞] で定義された振動における変位とすると，上記は角周波数をω，振幅を A (ω)，初期位相を φ (ω), (ω > 0) とする正弦波と，直流成分 F (0) / (2π) の重ね合わせで f (t) を表せる事を示している．

Note: 以上述べた通り，フーリエ級数及びフーリエ変換は，ある波形の振動を正弦波の重ね合わせによって表現する際の，各正弦波の振幅，及び初期位相を示している．振動の分析にフーリエ解析を利用する際の目的によっては，角周波数と振幅の関係にしか興味が無い場合もあるが，特定分野の技術者向けの解説書ならいざ知らず，教科書レベルの文献において，初期位相は重要では無いと言った記述が散見されて仰天している．正弦波を合成した際に得られる波形は，各正弦波の振幅と初期位相に依存する．従って，振動を正弦波の重ね合わせによって表現する際に必要となる情報は，各正弦波の角周波数，振幅，及び初期位相となる．

フーリエ逆変換の収束

区間 [−∞, ∞] で定義された関数 f (t) が以下の式を満たす場合，f (t) を絶対積分可能な関数と言う．

$\begin{matrix} (8-24) & \int_{- \infty}^{\infty} |f (t)| d t < \infty \end{matrix}$

関数 f (t) が絶対積分が可能，かつ区分的に連続，区分的に滑らかな場合，関数 f (t) のフーリエ変換 F (ω) が存在する．また，その場合のフーリエ逆変換の収束を以下に示す．

連続な点における f (t) のフーリエ逆変換は f (t) に収束する．
不連続な点における f (t) のフーリエ逆変換は，下記の通り，不連続点の左側極限値と右側極限値の平均に収束する．

$\begin{matrix} (8-25) & F^{- 1} [F (ω)] = \frac{f (t - 0) + f (t + 0)}{2} \end{matrix}$

即ち，フーリエ級数と同様に，フーリエ逆変換も，連続な点は厳密に表現できるが，不連続点は元の関数の近似となり，これを厳密に表現する事は出来ない．

フーリエ変換の定理

フーリエ変換の主要な定理を以下に示す．

**表8-1: フーリエ変換の主要な定理．**
線形性	$F [a f (t) + b g (t)] = a F [f (t)] + b F [g (t)] = a F (ω) + b G (ω)$
縮　　尺	$F [f (a t)] = \frac{1}{\|a\|} F (\frac{ω}{a})$
対称性	$F [F (t)] = 2 π f (- ω)$
微　　分	$F [\frac{d}{d t} f (t)] = j ω F (ω)$
畳み込み	$F [\int_{- \infty}^{\infty} f (t - τ) g (τ) d τ] = F (ω) G (ω)$
パーセバルの定理	$\int_{- \infty}^{\infty} {\|f (t)\|}^{2} d t = \frac{1}{2 π} \int_{- \infty}^{\infty} {\|F (ω)\|}^{2} d ω$
時間軸のシフト	$F [f (t - a)] = e^{- j a ω} F [f (t)] = e^{- j a ω} F (ω)$
周波数軸のシフト	$F [e^{- j a t} f (t)] = F (ω + a)$

以下に続く．

8. フーリエ級数展開とフーリエ変換 (続き) - 趣味人のブログ